 por camila_braz » Dom Jun 11, 2017 11:42
por camila_braz » Dom Jun 11, 2017 11:42
Boa tarde!
A questão pede para que eu calcule
![\lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/3cfa769e52843709139b192bb3a561e4.png)
Eu tentei dividir tudo por

![\frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/a45c96b809854be49e2077e8bde19e5b.png)
Ficando assim o numerador:
![\frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}} \frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}}](/latexrender/pictures/31deac1ec23061affd81a9aa50a37f4b.png)
=
![\sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}} \sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}}](/latexrender/pictures/8583a847d4bacb8770ced2578924f473.png)
E o denominador:
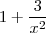
Então como a divisão por infinito tende a zero, eu encontrei:
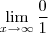
= 0
Isso está correto? Abraços.
-
camila_braz
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Jun 11, 2017 11:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE] Limites que tendem ao infinito com raízes
por Mell » Qua Mai 01, 2013 15:21
- 3 Respostas
- 2866 Exibições
- Última mensagem por e8group

Sáb Mai 04, 2013 02:41
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3527 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito] Com raizes!!
por J0elKim » Seg Abr 22, 2013 16:57
- 0 Respostas
- 1218 Exibições
- Última mensagem por J0elKim

Seg Abr 22, 2013 16:57
Cálculo: Limites, Derivadas e Integrais
-
- limites- Limite no infinito
por killerkill » Dom Ago 21, 2011 14:13
- 1 Respostas
- 1654 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [limites] limite no infinito
por baloso » Qua Abr 30, 2014 17:19
- 3 Respostas
- 2105 Exibições
- Última mensagem por Russman

Qui Mai 01, 2014 15:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/3cfa769e52843709139b192bb3a561e4.png)

![\frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/a45c96b809854be49e2077e8bde19e5b.png)
![\frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}} \frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}}](/latexrender/pictures/31deac1ec23061affd81a9aa50a37f4b.png) =
= ![\sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}} \sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}}](/latexrender/pictures/8583a847d4bacb8770ced2578924f473.png)
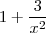
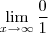 = 0
= 0
![\lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \lim_{x\rightarrow\infty} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/3cfa769e52843709139b192bb3a561e4.png)

![\frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3} \frac{\sqrt[2]{x} + \sqrt[3]{x} }{x^2+3}](/latexrender/pictures/a45c96b809854be49e2077e8bde19e5b.png)
![\frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}} \frac{\sqrt[2]{x}}{\sqrt[2]{x^4}} + \frac{\sqrt[3]{x}}{\sqrt[3]{x^6}}](/latexrender/pictures/31deac1ec23061affd81a9aa50a37f4b.png) =
= ![\sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}} \sqrt[2]{\frac{1}{x^3}} + \sqrt[3]{\frac{1}{x^5}}](/latexrender/pictures/8583a847d4bacb8770ced2578924f473.png)
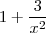
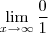 = 0
= 0