 por zenildo » Qui Dez 29, 2016 21:10
por zenildo » Qui Dez 29, 2016 21:10
Esse problema tentei resolver mas não consegui. É da minha irmã. Alguém?
- Anexos
-

-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por adauto martins » Seg Jan 02, 2017 15:22
por adauto martins » Seg Jan 02, 2017 15:22
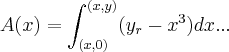
,onde
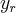
é a equaçao da reta a ser determinda e
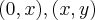
serao os pontos de intersecçao da reta com o eixo x,e interseçao da reta com a curva
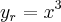
,q. sera o intervalo de integraçao...determine-os...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Qui Jan 05, 2017 11:05
por adauto martins » Qui Jan 05, 2017 11:05
vamos a soluçao desse problema:
a equaçao da reta tangente:
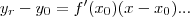
,como foi dado o ponto (0,2)
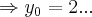
o ponto
![(\sqrt[3]{2},2)\in {y}_{r},{x}^{3} (\sqrt[3]{2},2)\in {y}_{r},{x}^{3}](/latexrender/pictures/58e5e36c41810e23134dd266ed180282.png)
,logo a equaçao da reta tangente sera:
![{y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})... {y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})...](/latexrender/pictures/0b6112b3bcce2ff7b5bda5398407d76c.png)
os pontos onde
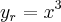
,serao os limites de integraçao da integraçao em questao:
![3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0 3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0](/latexrender/pictures/7cc98a7e379c84a6a628982bb0c0ece8.png)
,ai agora é resolver essa equaçao de terceiro grau...
bom pra resolver isso pode-se usar a reduçao de polinomios,caso tenha raizes complexas havera somente uma raiz real,caso esse q. nao resolve o problema pois precisa de duas raizes reais q. serao os limites da integral,ou entao usar a formula do calculo de raizes da eq. de terceiro grau...ai meu caro é com vcs,maos a obra...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



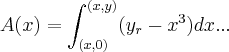 ,onde
,onde 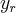 é a equaçao da reta a ser determinda e
é a equaçao da reta a ser determinda e 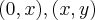 serao os pontos de intersecçao da reta com o eixo x,e interseçao da reta com a curva
serao os pontos de intersecçao da reta com o eixo x,e interseçao da reta com a curva 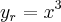 ,q. sera o intervalo de integraçao...determine-os...
,q. sera o intervalo de integraçao...determine-os...
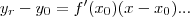 ,como foi dado o ponto (0,2)
,como foi dado o ponto (0,2) 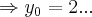
![(\sqrt[3]{2},2)\in {y}_{r},{x}^{3} (\sqrt[3]{2},2)\in {y}_{r},{x}^{3}](/latexrender/pictures/58e5e36c41810e23134dd266ed180282.png) ,logo a equaçao da reta tangente sera:
,logo a equaçao da reta tangente sera:![{y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})... {y}_{r}-2=f'(\sqrt[3]{2})(x-\sqrt[3]{2})...](/latexrender/pictures/0b6112b3bcce2ff7b5bda5398407d76c.png) os pontos onde
os pontos onde 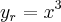 ,serao os limites de integraçao da integraçao em questao:
,serao os limites de integraçao da integraçao em questao:![3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0 3.(\sqrt[3]{2})^{2}).(x-\sqrt[3]{2})+2={x}^{3}\Rightarrow {x}^{3}-3.(\sqrt[3]{2})^{2}(x-\sqrt[3]{2})-2=0\Rightarrow
{x}^{3}-3.(\sqrt[3]{2})^{2})x+(3.\sqrt[3]{2}-2)=0](/latexrender/pictures/7cc98a7e379c84a6a628982bb0c0ece8.png) ,ai agora é resolver essa equaçao de terceiro grau...
,ai agora é resolver essa equaçao de terceiro grau...


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.