Alguém me pode dar uma ajuda com a seguinte integral dupla ?
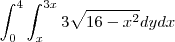
Sei que o resultado é 128, mas não consigo chegar nele.
Antecipadamente grato
Armando

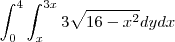

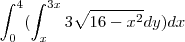
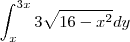 , numa calculadora TI-Nspire CX CAS, dá:
, numa calculadora TI-Nspire CX CAS, dá: 
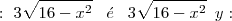

 . É que a integral desta expressão, com limites de
. É que a integral desta expressão, com limites de ![[0,4] [0,4]](/latexrender/pictures/b839c0a45fd15dac69be08a4dbb0b7e3.png) em relação a
em relação a  eu sei como resolver de modo a chegar no valor 128.
eu sei como resolver de modo a chegar no valor 128.
![I=\int_{0}^{4}(\int_{x}^{3x}3.\sqrt[]{(16-{x}^{2})}dy)dx=\int_{0}^{4}3.\sqrt[]{(16-{x}^{2})}(\int_{x}^{3x}dy)dx= I=\int_{0}^{4}(\int_{x}^{3x}3.\sqrt[]{(16-{x}^{2})}dy)dx=\int_{0}^{4}3.\sqrt[]{(16-{x}^{2})}(\int_{x}^{3x}dy)dx=](/latexrender/pictures/6f1361319c3c013ae03420b84d039edf.png)
![3.\int_{0}^{4}\sqrt[]{(16-{x}^{2})}(3x-x)dx=3.\int_{0}^{4}2x.\sqrt[]{(16-{x}^{2})}dx... 3.\int_{0}^{4}\sqrt[]{(16-{x}^{2})}(3x-x)dx=3.\int_{0}^{4}2x.\sqrt[]{(16-{x}^{2})}dx...](/latexrender/pictures/379488ca8fbf2724ff527fef0aa1db67.png) ,faz-se
,faz-se ![u=16-2x...du=-2xdx\Rightarrow I=-3.\int_{0}^{4}u.\sqrt[]{u}du=3.\int_{4}^{0}u.\sqrt[]{u}du... u=16-2x...du=-2xdx\Rightarrow I=-3.\int_{0}^{4}u.\sqrt[]{u}du=3.\int_{4}^{0}u.\sqrt[]{u}du...](/latexrender/pictures/c09dfe85ca490b4be867ce632b78f9eb.png) ,agora é usar a integraçao por partes,pois chegou-se a uma integral do produto de duas funçoes
,agora é usar a integraçao por partes,pois chegou-se a uma integral do produto de duas funçoes ![u.\sqrt[]{u} u.\sqrt[]{u}](/latexrender/pictures/0e882785540ed8252f05ad69f2891f4a.png) ,cuja formula é dado por:
,cuja formula é dado por: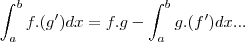 ,termine-o...
,termine-o...![u.\sqrt[]{u}={u}^{2}/\sqrt[]{u}... u.\sqrt[]{u}={u}^{2}/\sqrt[]{u}...](/latexrender/pictures/732940b1743fd5ffe64b9f680ac30805.png)



 como em derivadas parciais tbem...
como em derivadas parciais tbem...![I=3.\int_{0}^{4}2x.\sqrt[]{(16-{x}^{2})}dx I=3.\int_{0}^{4}2x.\sqrt[]{(16-{x}^{2})}dx](/latexrender/pictures/a8e7d090940f23c44c7fcc66ca4b005a.png) ,fizemos
,fizemos![u=16-{x}^{2}\Rightarrow du=-2xdx...I=-3.(\int_{0}^{4}\sqrt[]{(16-{x}^{2})}(-2xdx)=-3.\int_{0}^{4}\sqrt[]{u}du=-2.{u}^{3/2}[0,4]= u=16-{x}^{2}\Rightarrow du=-2xdx...I=-3.(\int_{0}^{4}\sqrt[]{(16-{x}^{2})}(-2xdx)=-3.\int_{0}^{4}\sqrt[]{u}du=-2.{u}^{3/2}[0,4]=](/latexrender/pictures/1aba37e376dd9b1f7d2f80e5e530fa08.png)
![-2.(\sqrt[]{(16-{x}^{2})}[0,4]=-2.(-64)=128... -2.(\sqrt[]{(16-{x}^{2})}[0,4]=-2.(-64)=128...](/latexrender/pictures/937203adc19d19c08888db852f4d25c0.png)


![\int\limit_{x}^{3x}(3\sqrt{16-x^2}) = (3\sqrt{16-x^2})y]^{3x}_{x} = 3x(3\sqrt{16-x^2}) - x(3\sqrt{16-x^2}) =\\
= (3x-x)\sqrt{16-x^2} = 2x(3\sqrt{16-x^2}) = 6x\sqrt{16-x^2} \int\limit_{x}^{3x}(3\sqrt{16-x^2}) = (3\sqrt{16-x^2})y]^{3x}_{x} = 3x(3\sqrt{16-x^2}) - x(3\sqrt{16-x^2}) =\\
= (3x-x)\sqrt{16-x^2} = 2x(3\sqrt{16-x^2}) = 6x\sqrt{16-x^2}](/latexrender/pictures/80fea566883b371cbf87b7fe85871fa8.png)

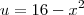
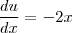
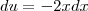

 para fora da integral, e a variável
para fora da integral, e a variável  que estava multiplicando por ele para junto de
que estava multiplicando por ele para junto de  , vamos ter:
, vamos ter: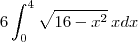
![6\int\limit_{0}^{\limit{4}}\sqrt{u}(-\frac{du}{2})\;\,=\;\,6\int\limit_{0}^{\limit{4}}{u}^{\frac{1}{2}}(-\frac{du}{2})\;\,=\;\,-\frac{6}{2}\int\limit_{0}^{\limit{4}}u^{\frac{1}{2}}du\;\,=\;\,-3\cdot\frac{u^{\frac{3}{2}}}{\frac{3}{2}}\,\,=\\
=\,\,\,-3\cdot\frac{2}{3}\cdot u^{\frac{3}{2}}\;\,=\;\,-\frac{6}{3}\cdot u^{\frac{3}{2}}=\,-2\cdot u^{\frac{3}{2}}\,=-2(16-x^2)^{\frac{3}{2}}=\,-2\sqrt{(16-x^2)^3}[{_{_0}^{^4}}=\\
=\,\,\,[-2\sqrt{(16-4^2)^3}]\,-\,[-2\sqrt{(16-0^2)^3}]\;\;=\;\,(0)\,\,-\,\,(-128)\;=\;\box{128} 6\int\limit_{0}^{\limit{4}}\sqrt{u}(-\frac{du}{2})\;\,=\;\,6\int\limit_{0}^{\limit{4}}{u}^{\frac{1}{2}}(-\frac{du}{2})\;\,=\;\,-\frac{6}{2}\int\limit_{0}^{\limit{4}}u^{\frac{1}{2}}du\;\,=\;\,-3\cdot\frac{u^{\frac{3}{2}}}{\frac{3}{2}}\,\,=\\
=\,\,\,-3\cdot\frac{2}{3}\cdot u^{\frac{3}{2}}\;\,=\;\,-\frac{6}{3}\cdot u^{\frac{3}{2}}=\,-2\cdot u^{\frac{3}{2}}\,=-2(16-x^2)^{\frac{3}{2}}=\,-2\sqrt{(16-x^2)^3}[{_{_0}^{^4}}=\\
=\,\,\,[-2\sqrt{(16-4^2)^3}]\,-\,[-2\sqrt{(16-0^2)^3}]\;\;=\;\,(0)\,\,-\,\,(-128)\;=\;\box{128}](/latexrender/pictures/a8f9e8458b49464aceb6ffb77c87cba7.png)

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes


 , avisa que eu resolvo.
, avisa que eu resolvo.

