mostre que Q
![sqrt[2] e Q sqrt[3]](/latexrender/pictures/9e6606822b66f83f46010ec762e0385b.png "sqrt[2] e Q sqrt[3]")
não são isomorfos.Sejam R e S aneis comutativos com unidade. Se
é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.(não sei nem como começar)
por daianalemos10 » Ter Jan 21, 2014 14:45
não são isomorfos. é um homomorfismo de R sobre S e a caracteristica de R é não nula, prove que a caracteristica de S divide a caracteristica de R.
por adauto martins » Qua Dez 28, 2016 17:08
{
},onde C é o conj.numeros complexos,a saber:
{![z=(x,y)/z=x+yi,i=\sqrt[]{-1}](/latexrender/pictures/621b7a84e98f5f7e57adb73c7a3e3dc7.png "z=(x,y)/z=x+yi,i=\sqrt[]{-1}")
}...vamos tomar 
e tal q.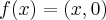
,entao:
,logo f e homomorfica...
,ou seja ,f é sobrejetiva,logo f é um isomorfismo...em geral,temos que: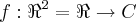
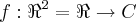
é um isomorfismo(prove isso!)...![f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]](/latexrender/pictures/2035eda00fcda6bc7e1c9095d9694ae2.png "f:Q[\sqrt[]{2}]\rightarrow Q[\sqrt[]{3}]")
,nao é um isomorfismo,pois:![Q[\sqrt[]{2}]=](/latexrender/pictures/a7256f5f86c336331eb74188f74ad173.png "Q[\sqrt[]{2}]=")
{![p+q\sqrt[]{2}](/latexrender/pictures/61adc756d326f219893de9b078683fbc.png "p+q\sqrt[]{2}")
![p+q\sqrt[]{2}/p,q \in Q](/latexrender/pictures/cc52592197311a5267ec9d00bbe70af5.png "p+q\sqrt[]{2}/p,q \in Q")
}...![Q[\sqrt[]{3}]=](/latexrender/pictures/e869a99ce70e7960638a95734722586d.png "Q[\sqrt[]{3}]=")
{![m+n\sqrt[]{3}/m,n \in Q](/latexrender/pictures/f0da65fec32e79ce293c569b21656290.png "m+n\sqrt[]{3}/m,n \in Q")
}... seja um isomorfismo,logo:![f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3}](/latexrender/pictures/631669dab169909fdb971959704d4b08.png "f(2)=f(\sqrt[]{2}.\sqrt[]{2})=a+b\sqrt[]{3}")
,como f é um isomorfismo,teriamos entao q.:![f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/cee47d65bc316d4028a33a0f72c3400f.png "f(1)=1...f(2)=f(1+1)=f(1)+f(1)=2...se:
[tex]{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)")
![{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)](/latexrender/pictures/f5721acbc42bcd3a03838d7e3c668b6a.png "{f(2)}^{2}={(a+b\sqrt[]{3}})^{2}\Rightarrow 4={a}^{2}+2.ab\sqrt[]{3}+3.{b}^{2}...\sqrt[]{3}=(4-3.{b}^{2})/a.b,p/a,b\neq 0...(4-3.{b}^{2})/a.b \in Q(racionais)")
,logo uma contradiçao...entao f nao é um homomorfismo,e como consequencia nao é um isomorfismo...
é por hipotese um homomorfismo,logo é injetivo,entao:![NUC[\phi]=](/latexrender/pictures/e714dcd144369ad5f1d4e28d9e6d9038.png "NUC[\phi]=")
{
}...entao:
existe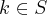 
,tal que k divide 
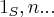,como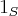 
divide apenas ele proprio,logo n=km...
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
.
: