 por Hoteri » Seg Dez 05, 2016 23:56
por Hoteri » Seg Dez 05, 2016 23:56
Boa noite, amigos. Há muito tempo tento resolver este problema:
Seja
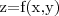
. Considere

. Calcule

se
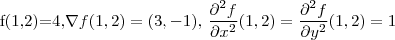
e

.
Primeiramente, calculei
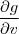
:

E, então,

:

Não sei se estou fazendo isto corretamente. Sou novo nesta área do Cálculo e, no meio do caminho da resolução, sinto que me perdi e não sei como prosseguir a partir daqui ou relacionar com os dados disponibilizados no enunciado. Agradeço a ajuda desde já.
-
Hoteri
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Dez 05, 2016 23:39
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por adauto martins » Qui Dez 08, 2016 09:09
por adauto martins » Qui Dez 08, 2016 09:09
primeiramente vamos encontrar uma expressao para

usando as condiçoes a),b)...
a diferencial total de

é dado por:
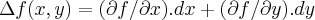
...com a condiçao b)teremos:

,onde c é devido a integraçao indefinida...usando a condiçao a)
,logo:
,usandos as outras condiçoes procede-se o calculo da derivada mista,calcule-o...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cálculo II - Regra da Cadeia para várias variáveis
por Guga1981 » Qua Nov 11, 2020 02:22
- 3 Respostas
- 4442 Exibições
- Última mensagem por Guga1981

Dom Nov 22, 2020 05:02
Cálculo: Limites, Derivadas e Integrais
-
- Regra da Cadeia 3 Variaveis Urgente
por Silva339 » Ter Mar 19, 2013 22:27
- 2 Respostas
- 2552 Exibições
- Última mensagem por Silva339

Qua Abr 03, 2013 18:24
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:28
- 1 Respostas
- 2264 Exibições
- Última mensagem por adauto martins

Qui Dez 25, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:33
- 1 Respostas
- 1975 Exibições
- Última mensagem por adauto martins

Ter Dez 23, 2014 16:28
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo de derivada com várias variáveis
por Fernandobertolaccini » Sex Dez 19, 2014 17:44
- 2 Respostas
- 2367 Exibições
- Última mensagem por adauto martins

Qua Dez 24, 2014 11:36
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Considere
. Considere  . Calcule
. Calcule  se
se 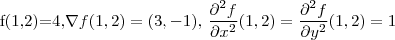 e
e  .
.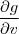 :
:
 :
:


 usando as condiçoes a),b)...
usando as condiçoes a),b)...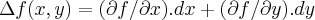 ...com a condiçao b)teremos:
...com a condiçao b)teremos: ,onde c é devido a integraçao indefinida...usando a condiçao a)
,onde c é devido a integraçao indefinida...usando a condiçao a)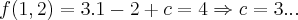 ,logo:
,logo: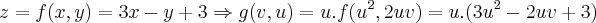
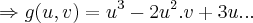 ,usandos as outras condiçoes procede-se o calculo da derivada mista,calcule-o...
,usandos as outras condiçoes procede-se o calculo da derivada mista,calcule-o...