 por useredu » Sex Set 02, 2016 11:55
por useredu » Sex Set 02, 2016 11:55
Bom dia,
Por favor não estou conseguindo deduzir está fórmula a partir da imagem do triângulo, se alguém conseguir e puder postar agradeço, será de grande ajuda


-
useredu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Set 02, 2016 11:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Producão
- Andamento: cursando
 por adauto martins » Qua Set 07, 2016 17:03
por adauto martins » Qua Set 07, 2016 17:03
tomamos a soma vetorial das forças

:
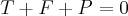
,pois os vetores formam um triang. fechado...
tomando o plano cartesiano como referencial e decompondo

,em
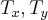
,teremos:
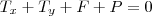


...como
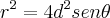
,teremos:

,tomando como pede o exercicio

,
teremos como se pede:
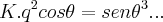
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por useredu » Qui Set 08, 2016 13:47
por useredu » Qui Set 08, 2016 13:47
adauto martins escreveu:tomamos a soma vetorial das forças

:
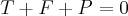
,pois os vetores formam um triang. fechado...
tomando o plano cartesiano como referencial e decompondo

,em
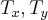
,teremos:
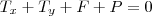


...como
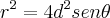
,teremos:

,tomando como pede o exercicio

,
teremos como se pede:
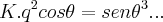
Muito obrigado mesmo! Foi de grande ajuda!
-
useredu
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sex Set 02, 2016 11:51
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Producão
- Andamento: cursando
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dedução de formula
por rodrigosoaresd » Ter Ago 14, 2012 14:30
- 1 Respostas
- 1695 Exibições
- Última mensagem por e8group

Ter Ago 14, 2012 15:34
Geometria Analítica
-
- [artigo] Uma dedução comentada da fórmula de Bhaskara
por admin » Qui Mai 15, 2008 15:44
- 0 Respostas
- 5756 Exibições
- Última mensagem por admin

Qui Mai 15, 2008 15:44
Cálculo
-
- Dedução
por Guilherme Carvalho » Qua Ago 10, 2011 22:40
- 1 Respostas
- 1658 Exibições
- Última mensagem por Molina

Qua Ago 10, 2011 23:49
Trigonometria
-
- Dedução
 por silvanuno11 » Ter Mar 27, 2012 13:26
por silvanuno11 » Ter Mar 27, 2012 13:26
- 0 Respostas
- 995 Exibições
- Última mensagem por silvanuno11

Ter Mar 27, 2012 13:26
Álgebra Elementar
-
- Dedução de Eq. de Reta
por OtavioBonassi » Qua Jan 05, 2011 22:40
- 3 Respostas
- 2740 Exibições
- Última mensagem por OtavioBonassi

Qui Jan 06, 2011 20:43
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 :
: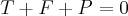 ,pois os vetores formam um triang. fechado...
,pois os vetores formam um triang. fechado... ,em
,em 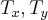 ,teremos:
,teremos: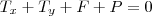

 ...como
...como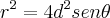 ,teremos:
,teremos: ,tomando como pede o exercicio
,tomando como pede o exercicio  ,
,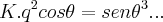

:
,pois os vetores formam um triang. fechado...
,em
,teremos:
...como
,teremos:
,tomando como pede o exercicio
,


 .
.



