Em um conjunto de 10.000 indivíduos de uma população, constatou-se que entre 4500 ganham menos de 3 salários mínimos, 4000 entre 3 e 5 (excluso o 5), 1000
entre 5 e 7 e 500 com mais de 7 salários mínimo. Determine a probabilidade de um indivíduo escolhido ao acaso dessa população ganhar:
O meu raciocínio sobre essas questões abaixo foi o seguinte
a) entre 3 e 5 salários mínimos (excluso 5).
4000 e 10000 correspondem a 40%
Então escolhendo um individuo do total, a chance de se obter uma pessoa que ganhe entre 3 e 5 salários mínimo é dada por

b) menos que 3 salários mínimos.
45 %

c) 5 ou mais salários mínimos.
Entre 5 e 7 - 10 %
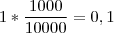
Mais de 7 - 5%
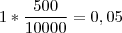
![P([5,7]) + P((7, \infty) P([5,7]) + P((7, \infty)](/latexrender/pictures/7c953b99570dc6d8b59337260211ff84.png) = 0.15 = 15%
= 0.15 = 15%d) mais de 7 salários mínimos.
Mais de 7 - 5%
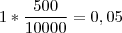
Quando eu analisava esse problema,cheguei até em pensar em usar o bínomio de Newton. Mas acabei chegando a conclusão de que isso não fazia sentido. Eu gostaria de saber se eu errei algum passo na resolução desse problema.
Segundo Problema
Obs: Para esse problema excluam a possibilidade de haver um empate.
Dois times de futebol, A e B, jogam entre si 6 vezes. Encontre a probabilidade de o time A:
a) Ganhar dois ou três jogos.
b) Ganhar pelo menos um jogo
Para a alternativa a eu usei o binômio de Newton, separei os valores da seguinte forma.
n = 6 Jogos. - número de experimentos aleatórios
K1 = 2 - probabilidade de um evento acontecer k vezes
k2 = 3 - probabilidade de um evento acontecer k vezes
P = 1/2 - Possibilidade de ganhar
q = 1/2 Possibilidade de perder
Calculando para dois jogos usando o binômio de newton o resultado foi: 15/64 = 23,438%
Calculando para três jogos usando o binômio de newton o resultado foi: 20/64 = 31,25%
A probabilidade de ganhar 2 ou 3 jogos
P(k1) + P(k2) = 15/64 + 20/64 <=> 23,438 + 31,25 = 54,688%
Calculando para um jogo usando o binômio de newton o resultado foi: 6/64 = 9,375%
Como os resultados obtidos, eu achei estranho a probabilidade de ganhar 3 jogos ser maior que a probabilidade de ganhar 2 e respectivamente 2 de 1. Eu acho que o correto seria que a probabilidade de ganhar 1 jogo deveria ser maior do que a de ganhar 2 e 3 e assim respectivamente. Com isso não tenho certeza se eu cometi algum erro no caminho.

