O problema é mais ou menos o seguinte:
Eu tenho um número X, e quero somar 10 a esse número X; digamos que X = 11 então por sua vez: 11 + 10 = 21
Agora, eu quero adicionar mais 10 a esse resultado, 21 + 10 = 31. E repetir isso Y vezes
Eu quero calcular o resultado da soma dessas operações todas.
Ex. (exemplo disso acontecendo 3 vezes [Y = 3]): (11 + 10) + (21 + 10) + (31 + 10) = 93
Como fazer isso, montar a equação e etc? Ou até melhor, quais tópicos/matérias eu devo estudar para me redimir como pessoa e calcular isso?
Fica registrado meu agradecimento desde já



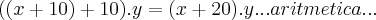

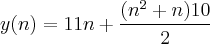
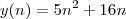 , mas deixei a fórmula "expandida" pra você ver como ela é montada e também para poder colocar outros valores diferentes de 11 e 10.
, mas deixei a fórmula "expandida" pra você ver como ela é montada e também para poder colocar outros valores diferentes de 11 e 10.
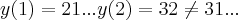 ...entao a formula de recorrencia naop responde a questao...
...entao a formula de recorrencia naop responde a questao...

 , avisa que eu resolvo.
, avisa que eu resolvo.

