 por Shambaloso » Qua Jul 06, 2016 19:54
por Shambaloso » Qua Jul 06, 2016 19:54
Olá, jovens, essa é minha primeira dúvida aqui, entao perdoem quaisquer erros de conduta, por favor. Vamos ao ex:
Sabendo que a altura de um triângulo relativa a hipotenusa é 12, exprima o comprimento da hipotenusa em função do perímetro de tal triângulo.
Chamemos os catetos de A e B, hipotenusa de C.
Por semelhança entre de triângulos vem: 12/A=B/C de onde B = 12C/A (I)
Substituindo B no Teorema de Pitágoras vem: 144C²/A² + A² = C² de onde acharíamos A em função de C para depois substituir em (I) e achar B em função de C.
Dessa forma, a equação do perímetro 2p = A + B + C ficaria em função de C, de onde poderíamos finalmente tirar a resposta do exercício.
O problema é aquela equação biquadrada que é gerada pelo teorema de pitágoras, cuja solução leva a uma resolução extremamente trabalhosa. Por isso estou em dúvida se minha abordagem está correta e/ou se há mais jeitos de fazer o exercício.
Desde já obrigado!
-
Shambaloso
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jul 06, 2016 19:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Medicina
- Andamento: cursando
 por adauto martins » Sáb Jul 09, 2016 18:11
por adauto martins » Sáb Jul 09, 2016 18:11
sejam x,y,h,os lados de um triangulo,no caso retangulo,pois foi dado q. a hipotenusa,tem uma relaçao de 12 com altura deste...vamos chamar y=altura,h=hipotenusa...o perimetro é a soma dos lados,entao...

...
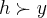
(por que?)
![\Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}} \Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}}](/latexrender/pictures/c858fdd4d35b3174f65eee55d0cc0f35.png)
...o problema pede
![p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h](/latexrender/pictures/73b7d4a4e68ba584ee894fce7eb3be48.png)
...ai é fazer as contas e...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Shambaloso » Sáb Jul 09, 2016 19:42
por Shambaloso » Sáb Jul 09, 2016 19:42
Não amigo, no enunciado consta que a altura relativa a hipotenusa é 12 (unidades, centimetros, metros, o que vc preferir), e não que a hipotenusa é 12 vezes o comprimento da altura.
-
Shambaloso
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Jul 06, 2016 19:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Medicina
- Andamento: cursando
 por adauto martins » Dom Jul 10, 2016 11:03
por adauto martins » Dom Jul 10, 2016 11:03
pois é meu caro,isso mesmo q. fiço...uma relaçao de proporcionalidade,nao vejo outra,pelo enunciado do problema...sedo um triang.retangulo(pq o enunciado diz hipotenusa) a hipotenusa é sempre maior q. os catetos,pisso
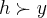
...logo teremos:
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13) p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)](/latexrender/pictures/f3ee42eb2b73b0e82a967949a486d678.png)
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26 p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26](/latexrender/pictures/a7539ee6e5341404e0b3268d2c009655.png)
![\Rightarrow h=(6/13).(13-\sqrt[]{143})p \Rightarrow h=(6/13).(13-\sqrt[]{143})p](/latexrender/pictures/1420d983723b87d9cf63dbe89758cd0a.png)
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como calcular o Perímetro sabendo-se somente a Hipotenusa
por macedo1967 » Qua Nov 29, 2017 11:03
- 2 Respostas
- 3318 Exibições
- Última mensagem por macedo1967

Ter Dez 05, 2017 18:41
Geometria Plana
-
- Geometria - Caixa Bombons Perimetro base e Altura
por Mike351 » Dom Jun 15, 2014 16:06
- 0 Respostas
- 2221 Exibições
- Última mensagem por Mike351

Dom Jun 15, 2014 16:06
Geometria Plana
-
- Achar catetos pela hipotenusa e pela altura
 por gustavoluiss » Dom Dez 05, 2010 23:44
por gustavoluiss » Dom Dez 05, 2010 23:44
- 5 Respostas
- 8607 Exibições
- Última mensagem por gustavoluiss

Seg Dez 06, 2010 20:37
Geometria Plana
-
- Perímetro do triângulo
por maria cleide » Sáb Mai 28, 2011 16:49
- 3 Respostas
- 3908 Exibições
- Última mensagem por MarceloFantini

Dom Mai 29, 2011 19:55
Geometria Plana
-
- Perímetro do triângulo
por leticiadelduque » Dom Ago 21, 2011 12:02
- 2 Respostas
- 1727 Exibições
- Última mensagem por leticiadelduque

Dom Ago 21, 2011 17:02
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ...
...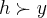 (por que?)
(por que?)![\Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}} \Rightarrow h=12y\Rightarrow x=\sqrt[]{{h}^{2}-{y}^{2}}](/latexrender/pictures/c858fdd4d35b3174f65eee55d0cc0f35.png) ...o problema pede
...o problema pede ![p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h p=f(h)\Rightarrow p=\sqrt[]{{h}^{2}-{(h/12)}^{2}}+h/12+h](/latexrender/pictures/73b7d4a4e68ba584ee894fce7eb3be48.png) ...ai é fazer as contas e...
...ai é fazer as contas e...
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13) p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)](/latexrender/pictures/f3ee42eb2b73b0e82a967949a486d678.png)
![p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26 p=(\sqrt[]{143}h/12)+13/12h=h/12(\sqrt[]{143}+13)\Rightarrow h=12p/(\sqrt[]{143}+13)\Rightarrow h=12p.(\sqrt[]{143}-13)/(143-169)=12p.(13-\sqrt[]{143})/26](/latexrender/pictures/a7539ee6e5341404e0b3268d2c009655.png)
![\Rightarrow h=(6/13).(13-\sqrt[]{143})p \Rightarrow h=(6/13).(13-\sqrt[]{143})p](/latexrender/pictures/1420d983723b87d9cf63dbe89758cd0a.png) ...
... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.