 por Bruhh » Seg Mar 08, 2010 16:31
por Bruhh » Seg Mar 08, 2010 16:31
Sendo A=

e B=

, calcular matriz X, tal que A.X=B
Então tentei resolver essa questão de várias maneiras mas todas sem sucesso.Multipliquei a matriz A pela sua inversa, multipliquei toda a conta pela inversa de A, enfim tentei de várias formas mas não consegui resolver.Será que alguem poderia me explicar?
Grata
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Molina » Seg Mar 08, 2010 16:33
por Molina » Seg Mar 08, 2010 16:33
Boa tarde,
Confirme, a matriz B tem apenas 2 (dois) elementos?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Bruhh » Seg Mar 08, 2010 21:31
por Bruhh » Seg Mar 08, 2010 21:31
Sim, exatamente, a matriz B possui apenas dois elementos.
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Bruhh » Qua Mar 10, 2010 14:31
por Bruhh » Qua Mar 10, 2010 14:31
Alguém poderia me ajudar??
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Neperiano » Qua Mar 10, 2010 15:08
por Neperiano » Qua Mar 10, 2010 15:08
Ola
Bruhh escreveu:Sendo A=

e B=

, calcular matriz X, tal que A.X=B
Então tentei resolver essa questão de várias maneiras mas todas sem sucesso.Multipliquei a matriz A pela sua inversa, multipliquei toda a conta pela inversa de A, enfim tentei de várias formas mas não consegui resolver.Será que alguem poderia me explicar?
Grata
A=

vezes x =

,= C

,
Olha tem muitos modos de fazer isso, eu fiz assim,
Primeiro a matriz X, deve ser 2:1, pq a matriz a é 2:2 e a matriz c é 2:1
segundo, considere na matriz x, o termo 1a como x e o termo 2a como y.
Eu fiz assim que x multiplicado por 4 e y multiplicado por 1 pode dar 24, e juntamente que x multiplicado por 2 e y multiplicado por -1 pode dar 6, encontrei, 5 e 4 respecitvamente, se quiser tente.
Acredito que por sistema de equações tambem da para fazer, se quiser tente, mas axo assim mais pratico
Qualquer duvida
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qua Mar 10, 2010 16:26
por MarceloFantini » Qua Mar 10, 2010 16:26
Apenas explicando o que o Maligno disse: para ter um produto de matrizes, o número de
colunas da primeira deve ser igual ao número de
linhas da segunda, por isso que a matriz X tem que ser
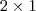
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Bruhh » Qui Mar 11, 2010 14:19
por Bruhh » Qui Mar 11, 2010 14:19
Ahh agora eu entendi, foi difícil mas eu consegui entender sim.
Fiz e deu certinho.
Muito Obrigada
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Neperiano » Qui Mar 11, 2010 15:50
por Neperiano » Qui Mar 11, 2010 15:50
Oi
Aki ta tudo entre colegas, vc faz engenharia eu tmb, hehehehehe
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Conversão de Unidades
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matriz Inversa
por Cleyson007 » Qui Ago 20, 2009 17:49
- 5 Respostas
- 4482 Exibições
- Última mensagem por Cleyson007

Sáb Ago 22, 2009 10:45
Matrizes e Determinantes
-
- [Matriz Inversa]
por vanessafey » Seg Set 12, 2011 15:17
- 4 Respostas
- 3283 Exibições
- Última mensagem por LuizAquino

Qua Set 21, 2011 23:23
Matrizes e Determinantes
-
- Matriz Inversa
por Claudin » Qui Set 15, 2011 17:44
- 11 Respostas
- 5274 Exibições
- Última mensagem por MarceloFantini

Qui Set 15, 2011 18:51
Matrizes e Determinantes
-
- Inversa da Matriz
por brunojorge29 » Seg Out 10, 2011 09:48
- 4 Respostas
- 2912 Exibições
- Última mensagem por brunojorge29

Qua Out 12, 2011 17:30
Matrizes e Determinantes
-
- Matriz inversa
por ViniRFB » Sex Mar 09, 2012 14:33
- 1 Respostas
- 1397 Exibições
- Última mensagem por ViniRFB

Sex Mar 09, 2012 14:49
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e B=
e B= , calcular matriz X, tal que A.X=B
, calcular matriz X, tal que A.X=B


 ,= C
,= C
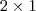 .
.