se f é uma função par e contínua no intervalo [-a,a] então:
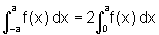
Gostaria de saber como eu faço pra chegar no resultado, se possível digam o passo a passo e quais regras eu devo usar, e fundamental saber isso na disciplina.

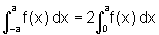

 para todo x . Faça o esboço do gráfico de alguns exemplos
para todo x . Faça o esboço do gráfico de alguns exemplos 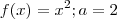 ,
, 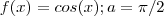 para fixar ideias ..Qual o comportamento de função continua par genérica num compacto simétrico
para fixar ideias ..Qual o comportamento de função continua par genérica num compacto simétrico ![[-2,2] , [-5,5], -[20,20] ou [-a,a] [-2,2] , [-5,5], -[20,20] ou [-a,a]](/latexrender/pictures/6edcd7b7de1eb7062e7418a51ab9d85a.png) ...O que significa
...O que significa 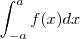 geometricamnete??? Corresponde a area com sinal da area delimitada pela gráfico da função , eixo x , e as retas verticais x = -a e x = a ... So para fixar ideias supor
geometricamnete??? Corresponde a area com sinal da area delimitada pela gráfico da função , eixo x , e as retas verticais x = -a e x = a ... So para fixar ideias supor  .. Chame a região de R .. Assim ,
.. Chame a região de R .. Assim , 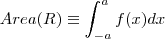 ..Esta região se decompõe como união de duas regiões
..Esta região se decompõe como união de duas regiões 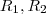 cuja interseção é uma região tem medida (area) nula .. Quem são elas ??
cuja interseção é uma região tem medida (area) nula .. Quem são elas ?? 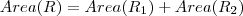 .. Observe que
.. Observe que 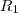 pode ser obtida reflexão como reflexão de
pode ser obtida reflexão como reflexão de 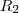 sobre o eixo y
sobre o eixo y 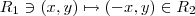 ... Intuitivamente ,
... Intuitivamente , 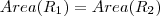 .. Logo
.. Logo 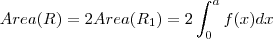 .. Isto é intuitivo e nos leva a conjeturar oq vc postou .. A prova por sua vez é bem simples .. Basta verificar que
.. Isto é intuitivo e nos leva a conjeturar oq vc postou .. A prova por sua vez é bem simples .. Basta verificar que 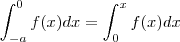 . Dica use o fato que f é par + faça uma subsituição
. Dica use o fato que f é par + faça uma subsituição 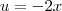 ...
...

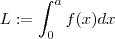 (Atenção a variável x é muda , de modo que
(Atenção a variável x é muda , de modo que 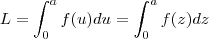 etc )
etc ) 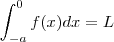 . Daí o resultado segue já que a integral de f sobre [-a,a] é a soma destas integrais .
. Daí o resultado segue já que a integral de f sobre [-a,a] é a soma destas integrais . 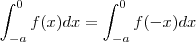 .
.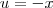 .Feito isto , verifique que (após trocar dx por -du e atualizar os limites de integração )
.Feito isto , verifique que (após trocar dx por -du e atualizar os limites de integração ) 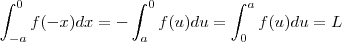 .
. 

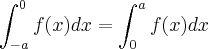 ...de fato,pois
...de fato,pois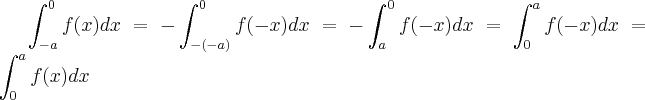 ...
...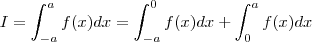 ,por a)teremos entao:
,por a)teremos entao: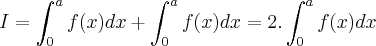 ...
...
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
