Seja W o espaço ortogonal de
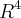 ortogonal a u1 = (1,1,2,2) e u2 = (0,1,2,-1). Encontre uma base ortogonal e uma base ortonormal de W. Sei que se eu encontrar uma base ortogonal para encontrar uma base ortonormal é só normalizar, certo?
ortogonal a u1 = (1,1,2,2) e u2 = (0,1,2,-1). Encontre uma base ortogonal e uma base ortonormal de W. Sei que se eu encontrar uma base ortogonal para encontrar uma base ortonormal é só normalizar, certo?Não sei como encontrar uma base ortogonal. Sei que para que dois vetores sejam ortogonais o produto interno entre eles deve ser zero. Mas não estou conseguindo usar essa informação para resolver o exercício. Grato quem puder ajudar.


 , a base canônica é formada por
, a base canônica é formada por  ; No
; No  , a base canônica é formada por
, a base canônica é formada por  . Então no
. Então no  , a base deverá ser formada por
, a base deverá ser formada por 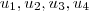 , desde que sejam L.I.
, desde que sejam L.I. :
: . Se a base é ortogonal, então
. Se a base é ortogonal, então  e
e  . Desta condição chegamos em
. Desta condição chegamos em  ; como pode notar, trata-se de um sistema indeterminado (escolha uma solução).
; como pode notar, trata-se de um sistema indeterminado (escolha uma solução). :
: . Se a base é ortogonal, então
. Se a base é ortogonal, então 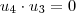 ,
,  e
e  ... (escolha uma solução).
... (escolha uma solução). e
e  fossem ortogonais, teríamos concluído o exercício; mas não são, e, para torná-los ortogonais podemos aplicar o
fossem ortogonais, teríamos concluído o exercício; mas não são, e, para torná-los ortogonais podemos aplicar o 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)