


 em radianos. A distância do "início" do eixo x à esquerda até o M deve ser a mesma distância de M até P (pois a reta inclinada faz um ângulo de 45 graus). Assim sendo, é razoável concluir que a distância de M até P é
em radianos. A distância do "início" do eixo x à esquerda até o M deve ser a mesma distância de M até P (pois a reta inclinada faz um ângulo de 45 graus). Assim sendo, é razoável concluir que a distância de M até P é 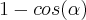 , lembrando que este ciclo trigonométrico tem raio 1.
, lembrando que este ciclo trigonométrico tem raio 1.

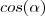 . Basta substituir.
. Basta substituir.
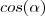 será negativo. Portanto, para a resposta ser o comprimento de M até P, é necessário mudar o sinal e o resultado fica
será negativo. Portanto, para a resposta ser o comprimento de M até P, é necessário mudar o sinal e o resultado fica 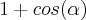 .
.

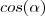 . Basta perceber que:
. Basta perceber que: , pois M0 é um comprimento que parte do ponto 0 no eixo dos cossenos e corresponde ao comprimento do arco.
, pois M0 é um comprimento que parte do ponto 0 no eixo dos cossenos e corresponde ao comprimento do arco.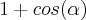 .
.




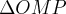 q.
q. 
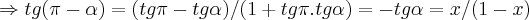
 e ai é isolar o x,resolva o restante...
e ai é isolar o x,resolva o restante...

 é isosceles...entao vamos á sol.correta:
é isosceles...entao vamos á sol.correta: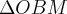 teremos:
teremos: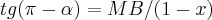 e
e ![MB=\sqrt[]{1-{(1-x)}^{2}} MB=\sqrt[]{1-{(1-x)}^{2}}](/latexrender/pictures/4a92363be3f661ba8b9950fa71b99f38.png) ,logo
,logo![tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x) tg(\pi-\alpha)=-tg\alpha=\sqrt[]{1-{(1-x)}^{2}}/(1-x)](/latexrender/pictures/8859129063dddefa5ac454130584debb.png) ...
...![-tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1 -tg\alpha=\sqrt[]{1-{(1-x)}^{2}/{(1-x)}^{2}}=\sqrt[]{1/{(1-x}^{2})-1}\Rightarrow {tg\alpha}^{2}=1/{(1-x)}^{2}-1](/latexrender/pictures/1c260b55ba4f302f93fe800138f819ea.png)

 ...
...
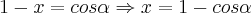 ...obrigado
...obrigado
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes