 por karenfreitas » Qua Mai 04, 2016 14:36
por karenfreitas » Qua Mai 04, 2016 14:36
Calcular o valor de A, onde A =
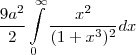
Usar
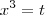

DEsde já agradeço quem puder ajudar a resolver esse problema.
-
karenfreitas
- Usuário Ativo

-
- Mensagens: 12
- Registrado em: Qua Mai 04, 2016 14:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por nakagumahissao » Sex Mai 06, 2016 00:54
por nakagumahissao » Sex Mai 06, 2016 00:54
![A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1] A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1]](/latexrender/pictures/0d1188185d3c7669e4e5f81f2fef6201.png)
Fazendo-se a substituição:

para:

e

tem-se que:
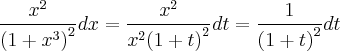
a integral desta fração seria:
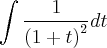
utilizando-se da seguinte substituição
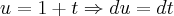
,
poderiamos resolver a integral acima da seguinte maneira:
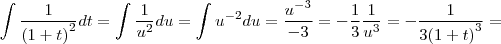
Mas,
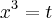
Logo,
![= -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2] = -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2]](/latexrender/pictures/f3872814f90bb18253c4f3d534a4b133.png)
Finalmente, utilizando-nos dos conhecimentos de integrais impróprias e usando [2] em 1, teremos:

![= \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = = \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] =](/latexrender/pictures/8c34ed89eae65f025bdfb7e00086b594.png)
![= -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2} = -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2}](/latexrender/pictures/d86c57d5afb1790a8408b296a56e5e4f.png)
Que é o resultado procurado, portanto:

Espero não ter errado nos cáculos, mas a idéia básica é essa.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Calculo] Calculando uma integral imprópria com uma condição
por karenfreitas » Sex Mai 06, 2016 15:10
- 0 Respostas
- 1965 Exibições
- Última mensagem por karenfreitas

Sex Mai 06, 2016 15:10
Cálculo: Limites, Derivadas e Integrais
-
- Calcular o seguinte limite
por RodrigoMan » Qua Jun 06, 2012 14:30
- 2 Respostas
- 2424 Exibições
- Última mensagem por RodrigoMan

Qua Jun 06, 2012 16:44
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular porcentagem do seguinte valor:?
por icaro » Ter Jan 23, 2018 12:23
- 1 Respostas
- 8500 Exibições
- Última mensagem por DanielFerreira

Qui Jan 25, 2018 11:31
Aritmética
-
- Gostaria de saber como calcular o seguinte limite
por felipe_08 » Qui Abr 23, 2015 17:36
- 2 Respostas
- 2581 Exibições
- Última mensagem por felipe_08

Qui Abr 23, 2015 22:51
Cálculo: Limites, Derivadas e Integrais
-
- Integral Imprópria
por CrazzyVi » Seg Set 27, 2010 17:13
- 5 Respostas
- 7250 Exibições
- Última mensagem por menino de ouro

Qui Jan 24, 2013 13:43
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
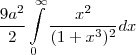
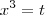


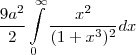
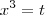


![A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1] A = \frac{9{a}^{2}}{2}\int_{0}^{\infty} \frac{{x}^{2}}{{\left(1+{x}^{3} \right)}^{2}} dx\;\;\;\;\;\;\;[1]](/latexrender/pictures/0d1188185d3c7669e4e5f81f2fef6201.png)



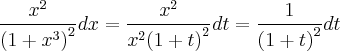
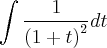
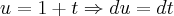 ,
,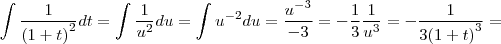
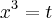
![= -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2] = -\frac{1}{3 {\left(1 + t \right)}^{3}} = -\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}}\;\;\;\;\;\;[2]](/latexrender/pictures/f3872814f90bb18253c4f3d534a4b133.png)

![= \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = = \frac{9{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{3 {\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = \frac{9{a}^{2}}{2}\left(-\frac{1}{3} \right) \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] =](/latexrender/pictures/8c34ed89eae65f025bdfb7e00086b594.png)
![= -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2} = -\frac{3{a}^{2}}{2} \lim_{m\rightarrow \infty} \left[-\frac{1}{{\left(1 + {x}^{3} \right)}^{3}} {|}_{0}^{m} \right] = -\frac{3{a}^{2}}{2}\left(-0 + 1 \right) = -\frac{3{a}^{2}}{2}](/latexrender/pictures/d86c57d5afb1790a8408b296a56e5e4f.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
