 por raimundosar » Qui Mai 05, 2016 19:02
por raimundosar » Qui Mai 05, 2016 19:02
Se uma função real de variável real f satisfaz à condição f(x) + 3f(2 - x) = x + 3 então:
a) f(x) = (x - 1)/4
b) f(x) = (x + 1)/3
c) f(x) = (3 - x)/2
d) f(x) = (x + 2)/5
e) f(x) = (2 - x)/6
-
raimundosar
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Mai 05, 2016 18:49
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Lic Matematica
- Andamento: formado
 por nakagumahissao » Sex Mai 06, 2016 00:25
por nakagumahissao » Sex Mai 06, 2016 00:25
f(x) + 3f(2 - x) = x + 3 [1]
Vamos calcular para x = 2 - x
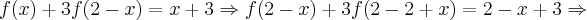
![\Rightarrow f(2-x) + 3f(x) = 5 - x \Rightarrow f(2-x) = 5 - x - 3f(x) \;\;\;[2] \Rightarrow f(2-x) + 3f(x) = 5 - x \Rightarrow f(2-x) = 5 - x - 3f(x) \;\;\;[2]](/latexrender/pictures/366179504a5a7db35f9d9b33a7a3b34a.png)
usando este último resultado [2] em [1], obtemos:
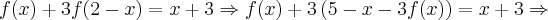
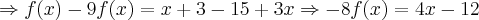
Dividindo-se ambos os lados desta última equação por (-4), obtem-se:
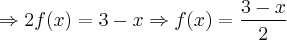
Portanto, a resposta procurada é a letra C.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5652 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
-
- Desafio dos Dez Pontos
 por Molina » Sáb Jul 12, 2008 00:02
por Molina » Sáb Jul 12, 2008 00:02
- 6 Respostas
- 5301 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 17:00
Desafios Fáceis
-
- Desafio de lógica
por Twister » Qua Ago 13, 2008 21:46
- 10 Respostas
- 10039 Exibições
- Última mensagem por andymath

Qua Mar 31, 2010 19:14
Desafios Enviados
-
- Desafio do relógio
por ericomoura » Ter Nov 17, 2009 12:03
- 9 Respostas
- 8319 Exibições
- Última mensagem por Dan

Qui Fev 10, 2011 12:21
Desafios Difíceis
-
- Desafio dos Dados
 por Molina » Dom Nov 22, 2009 13:07
por Molina » Dom Nov 22, 2009 13:07
- 5 Respostas
- 4479 Exibições
- Última mensagem por Douglasm

Seg Nov 01, 2010 19:58
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



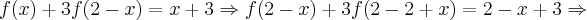
![\Rightarrow f(2-x) + 3f(x) = 5 - x \Rightarrow f(2-x) = 5 - x - 3f(x) \;\;\;[2] \Rightarrow f(2-x) + 3f(x) = 5 - x \Rightarrow f(2-x) = 5 - x - 3f(x) \;\;\;[2]](/latexrender/pictures/366179504a5a7db35f9d9b33a7a3b34a.png)
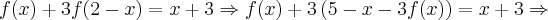
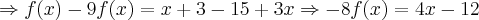
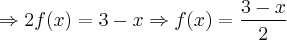

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.