Olá
Huovi! De acordo com minhas contas, a reta que encontrou não é a tangente. Veja como fiz:
Queremos encontrar a recta tangente da curva
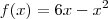
no ponto
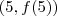
. Fazemos isso pela definição de limites ou pelo conceito de derivada. Farei por derivada, pois é menos trabalhoso!
Para encontrarmos a equação de uma recta tangente a uma curva dada, num determinado ponto, derivamos a equação da curva e substituímos a abscissa na derivada encontrada.

Como podes notar, temos a inclinação e um ponto, já somos capazes de descrever a equação da recta tangente.
Com isso, temos que

e

são as equações das rectas tangente e normal, respectivamente.
A meu ver, podes encontrar a área usando Geometria Plana e/ou Analítica. Use (base x altura)/2.



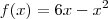 no ponto
no ponto 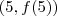 . Fazemos isso pela definição de limites ou pelo conceito de derivada. Farei por derivada, pois é menos trabalhoso!
. Fazemos isso pela definição de limites ou pelo conceito de derivada. Farei por derivada, pois é menos trabalhoso!
 e
e  são as equações das rectas tangente e normal, respectivamente.
são as equações das rectas tangente e normal, respectivamente.
