Nos problemas 1 e 2 são apresentados transformações lineares para cada uma delas determinar:
a) O núcleo,uma base desse subespaço e sua dimensão;
b) A imagem,uma base desse subespaço e sua dimensão;
1) f: R²?R²,f(x,y) = (3x-y,-3x+y)
2) f: R²?R³,f(x,y) = (x + y,x,2y)
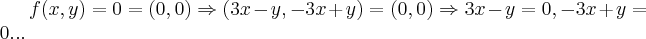
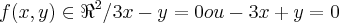}...tem-se q. a soluçao de S, é o vetor nulo,ou seja x=y=0,entao...![B=[\phi],DIM=0](/latexrender/pictures/9267d1809d3c7d23b90f0847fc3c0839.png "B=[\phi],DIM=0")
...![f(x,y)=(3x-y,-3x+y)=3x(1,-1)+y(-1,1)\Rightarrow B[(-1,1),(1-1)],DIM=2](/latexrender/pictures/b4f8756c81063f63f2e570b8fbf60471.png "f(x,y)=(3x-y,-3x+y)=3x(1,-1)+y(-1,1)\Rightarrow B[(-1,1),(1-1)],DIM=2")
...
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)