 por Pauloxppx » Sex Abr 22, 2016 12:01
por Pauloxppx » Sex Abr 22, 2016 12:01
Bom dia prezados,
Preciso entender porque esta questão chega neste resultado?
1- Sendo os conjuntos A=(-3,2], B= (-oo-2]U[2,oo) e C= {1,2,3,4}:
a) A X B , representado graficamente fica assim:
https://ap.imagensbrasil.org/image/ISBOR
-
Pauloxppx
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Abr 22, 2016 11:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Segurança da Informação
- Andamento: cursando
 por DanielFerreira » Sáb Abr 23, 2016 15:38
por DanielFerreira » Sáb Abr 23, 2016 15:38
Olá
Paulo, seja bem-vindo!
Ao representar um produto cartesiano no gráfico, deve estar ciente que os elementos dos conjuntos

e

são representados, respectivamente, nos eixos x e y; ou seja,
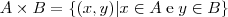
.
Note que os elementos do conjunto

estão entre
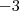
(exclusive) e

(inclusive). Já o conjunto

é dado por
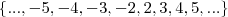
. A grosso modo, temos uma intersecção representada no gráfico!
Espero tê-lo ajudado!
Qualquer dúvida retorne.
Até!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto Cartesiano
por Cleyson007 » Seg Set 01, 2008 13:34
- 1 Respostas
- 7121 Exibições
- Última mensagem por admin

Seg Set 01, 2008 14:45
Conjuntos
-
- Produto Cartesiano
por Cleyson007 » Ter Set 02, 2008 13:08
- 3 Respostas
- 5577 Exibições
- Última mensagem por admin

Qui Set 04, 2008 15:40
Conjuntos
-
- Produto Cartesiano
por MaiSantos » Sex Set 09, 2011 10:19
- 1 Respostas
- 1301 Exibições
- Última mensagem por MarceloFantini

Sex Set 09, 2011 16:23
Funções
-
- Produto Cartesiano de Conjuntos
por tertulia » Qui Dez 30, 2010 20:24
- 0 Respostas
- 870 Exibições
- Última mensagem por tertulia

Qui Dez 30, 2010 20:24
Álgebra Elementar
-
- [Funções]Plano Cartesiano
 por ti123 » Qui Out 08, 2020 09:36
por ti123 » Qui Out 08, 2020 09:36
- 2 Respostas
- 7359 Exibições
- Última mensagem por DanielFerreira

Dom Out 25, 2020 16:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 e
e  são representados, respectivamente, nos eixos x e y; ou seja,
são representados, respectivamente, nos eixos x e y; ou seja, 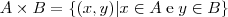 .
. estão entre
estão entre 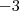 (exclusive) e
(exclusive) e  (inclusive). Já o conjunto
(inclusive). Já o conjunto  é dado por
é dado por 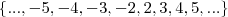 . A grosso modo, temos uma intersecção representada no gráfico!
. A grosso modo, temos uma intersecção representada no gráfico!