Após pegar a variável u e sua derivada,
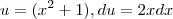, eu coloco na integral, com os valores limites recalculados, mas eu não consigo entender o por que o 
que esta fora do parenteses 'some' da integração, na proxima etapa onde eu iria colocar o 
para ser integrado, eu já coloco mais o .
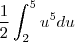
Por que, sendo que, se eu tivesse que calcular a anti-derivada do
, eu deveria colocar na equação p/ ser calculada também ?
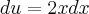o próximo passo será achar o valor de 
para substituir na integral, porque agora estará em função de 
Então ficará:![\[ \frac{du}{2x} \] = dx](/latexrender/pictures/2a20e8b8283ad295135ce3f45ce3e8d0.png "\[ \frac{du}{2x} \] = dx")
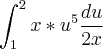
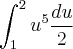
para fora Integral: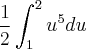
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")