 por CarolinaR » Seg Mar 07, 2016 11:00
por CarolinaR » Seg Mar 07, 2016 11:00
As raízes da equação x³-9x²+23x - 15 = 0 , colocadas em ordem crescente , são os termos iniciais de uma progressão aritmétcia cuja soma dos 10 primeiros termos é :
a)80
b)90
c)100
d)110
e)120
Tentei fazer descobrindo as raízes , para depois usar a fórmula da P.A para descobrir a soma dos 10 primeiros termos mas não deu certo , pois quando fui tirar as raízes por baskara , o delta deu negativo .
o jeito que eu tava tentando fazer :
x (x² - 9x + 23 ) - 15 = 0
x=15 ou delta = (-9)² - 4.1.23 = ?-11
Foi a única forma que pensei para resolvê - lo )=
-
CarolinaR
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mar 04, 2016 19:39
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Dom Abr 10, 2016 23:54
por DanielFerreira » Dom Abr 10, 2016 23:54
CarolinaR escreveu:As raízes da equação x³-9x²+23x - 15 = 0 , colocadas em ordem crescente , são os termos iniciais de uma progressão aritmética cuja soma dos 10 primeiros termos é :
a)80
b)90
c)100
d)110
e)120
Olá
Carolina, boa noite!
Considere a seguinte equação:

; uma possível raiz é dada pelos divisores (positivos e negativos) de

.
Nesse exercício, temos
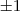
,
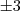
,

e

. Ao verificar se
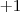
é uma das raízes, o resultado é verdadeiro.
Aplicando o
Dispositivo de Briot Rufini irá concluir que:

.
Por conseguinte, ao fatorar o segundo fator, tiramos que
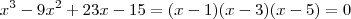
.
Já que as raízes foram obtidas, agora podemos obter a soma da P.A.
Tente concluir! Deverá encontrar 100.
Até.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UNIFOR) Progressão Aritmética e Progressão Harmônica
por andersontricordiano » Ter Mar 22, 2011 12:56
- 1 Respostas
- 6128 Exibições
- Última mensagem por LuizAquino

Ter Mar 22, 2011 13:52
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4720 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- [Aritmética] Progressão Aritmética.
por Pessoa Estranha » Qua Ago 28, 2013 22:11
- 2 Respostas
- 5625 Exibições
- Última mensagem por Pessoa Estranha

Qui Ago 29, 2013 16:06
Aritmética
-
- Progressão Aritmética
por Rejane Sampaio » Qua Set 17, 2008 16:20
- 1 Respostas
- 4418 Exibições
- Última mensagem por juliomarcos

Qui Set 18, 2008 13:07
Álgebra Elementar
-
- Progressão Aritmética (PA)
por Cleyson007 » Ter Jan 27, 2009 21:40
- 2 Respostas
- 8392 Exibições
- Última mensagem por Cleyson007

Sáb Mai 30, 2009 12:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ; uma possível raiz é dada pelos divisores (positivos e negativos) de
; uma possível raiz é dada pelos divisores (positivos e negativos) de  .
.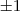 ,
, 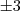 ,
,  e
e  . Ao verificar se
. Ao verificar se 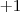 é uma das raízes, o resultado é verdadeiro.
é uma das raízes, o resultado é verdadeiro. .
.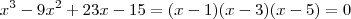 .
.