 por GehSillva7 » Qui Fev 25, 2016 12:55
por GehSillva7 » Qui Fev 25, 2016 12:55
Seja p > 0 um numero primo e seja Q[sqrt(p)] = {a+b sqrt(p); a, b E Q}. Defina as operações + e . em Q[ sqrt(p] como (a+b sqrt(p)) + (c + d sqrt(p)) = (a+c)+(b+d) sqrt(p) e (a+b sqrt(p)) . (c + d sqrt(p)) = (ac + pbd) + (ad+bc) sqrt(p). Mostre que Q[sqrt(p)] é um corpo.
-
GehSillva7
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Fev 23, 2014 21:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por adauto martins » Dom Fev 28, 2016 13:38
por adauto martins » Dom Fev 28, 2016 13:38
pelo q. pude traduzir do q. vc escreveu e mostrar q...Q={
![a+b\sqrt[]{p} a+b\sqrt[]{p}](/latexrender/pictures/99f8728343f5210cbbcb8401d4dd6adf.png)
,onde a,b,p
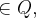
,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...
1)
![0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x 0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/a82f8aa2d2ad3922213cb5b75e3fc31a.png)
...
2)
![1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x 1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/bc2a4ec8df011955d665fbe042c2c6d8.png)
...
3)seja
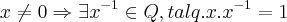
,de fato...
![x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1 x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1](/latexrender/pictures/a499118cc6998a170a2253c2069e29d3.png)
...as outras 5 sao mais facieis...verifique-as...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por GehSillva7 » Dom Fev 28, 2016 15:40
por GehSillva7 » Dom Fev 28, 2016 15:40
Show! Muito obrigada!
-
GehSillva7
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Dom Fev 23, 2014 21:50
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
Voltar para Aritmética
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



![a+b\sqrt[]{p} a+b\sqrt[]{p}](/latexrender/pictures/99f8728343f5210cbbcb8401d4dd6adf.png) ,onde a,b,p
,onde a,b,p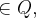 ,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...
,p primo}...bom,um corpo é um espaço vetorial de dimensao nula,entao temows aquelas 8 propriedades a ser verificadas,farei algumas,tdbem...![0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x 0\in Q, pois 0+x=(0+0\sqrt[]{p})+(a+b\sqrt[]{p})=(0+a)+(0+b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/a82f8aa2d2ad3922213cb5b75e3fc31a.png) ...
...![1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x 1\in Q,pois...1.x=(1+0\sqrt[]{p}).(a+b\sqrt[]{p})=(1.a+p.0)+(1.b+0.p.b)\sqrt[]{p}=a+b\sqrt[]{p}=x](/latexrender/pictures/bc2a4ec8df011955d665fbe042c2c6d8.png) ...
...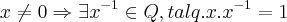 ,de fato...
,de fato...![x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1 x.{x}^{-1}=(a+b\sqrt[]{p}).(1/(a+b\sqrt[]{p})=(a+b\sqrt[]{p}).(a-b\sqrt[]{p})/({a}^{2}-p.{b}^{2})={a}^{2}-p.{b}^{2}/({a}^{2}-p.{b}^{2})=1](/latexrender/pictures/a499118cc6998a170a2253c2069e29d3.png) ...as outras 5 sao mais facieis...verifique-as...
...as outras 5 sao mais facieis...verifique-as...






