Potencias com expoentes diferentes - Subtrair?

[Soprano]

Olá,

Nas regras da potenciação não encontro resposta para esta minha dúvida. Também não sei se ela tem lógica, mas então cá vai..
Tenho a seguinte expressão:

5(3x? - 12x³) o resutado desta expressão é 5(9x)? Eu resolvi isto assim:

x? - x³ - como tem a mesma base e expoentes diferentes, subtrai as bases e os expoentes! Posso fazer isto?

Obrigado

[DanielFerreira]

Bom dia, Soprano. Seja bem-vindo!!

Não podes efectuar a subtração, pois os expoentes são diferentes.

Se me permite, sugiro que faça uma leitura sobre redução de termos semelhantes.

Até breve.

[Soprano]

Olá Daniel Ferreira,

Obrigado pela resposta,
Então neste caso terei que ir pela simplificação de polinómios para conseguir anular termos, correcto? Nota: Falta o resto do sistema, porque se a expressão fosse esta não haveria mais nada a fazer, certo?

Na tua resposta sugeres a leitura de redução de termos semelhantes Existe algum link, onde posso encontrar isso?

Obrigado

[Cleyson007]

Soprano, boa tarde!

Amigo DanielFerreira, aproveitando que estou online vou responder a mensagem

Nesse link você encontra uma explicação teórica e também alguns exercícios com resposta para praticar: http://jmpgeo.blogspot.com.br/2011/11/t ... antes.html

Bons estudos

Att,

Prof° Clésio

Caso queira conhecer melhor o meu trabalho, acesse: viewtopic.php?f=151&t=13614

[DanielFerreira]

Soprano,

na primeira indagação, eu trocaria as palavras "simplificação" e "anular" por redução; desse modo, a resposta é sim/correcto.

Na segunda, é isso mesmo; não teríamos mais nada a fazer.

Não deixe de acessar o link sugerido pelo professor Clésio.

Profº Clésio, fique à vontade.

[Soprano]

Ok, vou analisar os links,

O mesmo se aplica a esta situação, fruto do que estamos a debater no outro tópico:



Posso fazer mais alguma coisa aqui? Não, pois os expoentes são diferentes, certo?

[DanielFerreira]

Meu caro, isso não pode ser feito! Não podes "separar" o denominador dessa forma.

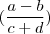Tomemos como exemplo . Repare que não é o mesmo que . Em matemática, diz-se que isso é um absurdo!

Se quisermos separar os termos do numerador, o que temos a fazer é o seguinte:



Se quiseres, podes atribuir valores numéricos à expressão e verificar que, de fato, .

[Soprano]

Ok, percebi,

Ainda relativamente à primeira questão numa subtração entre potencias com expoentes diferentes não posso fazer nada. Mas caso tenham o mesmo expoente, mas bases diferentes ou iguais, quais são as regras?
Pela lógica deve ser simples, basta adicionar ou subtrair as bases, certo?

Vamos imaginar este cenário:

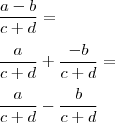
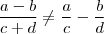isto será igual a certo?
Mas o resultado não é o mesmo, da primeira é 25 + 9 = 34. A segunda é 64.

Obrigado