Boa tarde, não obtive exito ao tentar resolver a questão abaixo pelo princípio fundamental da contagem. Haverei de recorrer às fórmulas mesmo? Ou há uma alternativa mais fácil?
(UFES 2013) 15ª QUESTÃO - A quantidade de números inteiros positivos de 4 algarismos (não necessariamente distintos) que podem ser escritos com os algarismos 1, 2, 3, 4, 5 e 6, de modo que o algarismo 1 aparece em cada número, mas não é o algarismo final do número, é:
A) 455
B) 405
C) 505
D) 555
E) 605
Assim eu pensei: como não são necessariamente números distintos, posso repetir: 6x6x6x5, o algarismo 1 não pode ser usado na última casa, então não o considero. Mas como atender à restrição "de modo que o algarismo 1 aparece em cada número"?


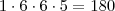 .
.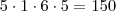 .
. .
.


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)