Olá
Ivo, seja bem-vindo!!
Pondo em ordem alfabética, a primeira palavra formada seria
CEEPSX; inicialmente, o que temos a fazer e descobrir a quantidade de anagramas que começam com C. Fixando essa letra na primeira posição, devemos permutar apenas as palavras seguintes, isto é, EEPSX.
A quantidade de anagramas de EEPSX é dada por:

O resultado encontrado corresponde à posição ocupada pelo último anagrama (ordem alfabética) das letras acima; ou seja, a palavra CXSPEE ocupa a 60ª posição.
Devemos, agora, encontrar a quantidade de anagramas que começam com EC. Aplicando raciocínio análogo ao anterior, tiramos que a quantidade de anagramas da palavra
ECEPSX que começam por EC é:
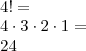
O resultado encontrado somado àquele, nos dá a posição ocupada pela palavra ECXSPE - que é 84ª.
A próxima quantidade de anagramas a ser contada é a que se inicia por EE; efectuando os mesmos cálculos acima chegamos a 24 anagramas.
A próxima quantidade ... inicia por EP; por motivo análogo, chegamos a 24 anagramas.
Enfim, chegamos a ES! Note que agora devemos analisar a sequência ESC, ESE, ESP.
Para ESC temos:
ESCEPX. Já que as três primeiras são fixas, temos de permutar apenas as três últimas; o que nos dá 6.
Para
ESEPSX, temos também 6 anagramas.
Por fim, temos
ESPCEX; ih!! a que queremos, portanto apenas 1 anagrama.
Somemos,
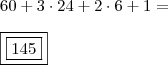




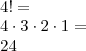
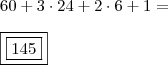


 .
.



