f(x,y,z) e g(x,y) são funções diferenciáveis tais que ,para todo (x,y) no domínio de g,f(x,y,g(x,y))=0.Suponha g(1,1)=3,derivadaparcialf/x(1,1,3)=2,derivadaparcialf/y(1,1,3)=5 e derivadaparcialf/z(1,1,3)= 10 . Determine a equação do plano tangente ao gráfico de g no ponto(1,1,3) .
não consigo resolver porque g é função de duas variáveis e o ponto pedido tem três coordenadas ,pensei então na f(1,1,g(1,1)) mas não consegui derivar f.


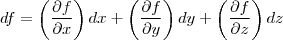
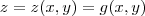 então
então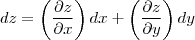



 , avisa que eu resolvo.
, avisa que eu resolvo.

