 por Fabricio dalla » Sáb Nov 14, 2015 21:21
por Fabricio dalla » Sáb Nov 14, 2015 21:21
olá pessoal,tenho uma duvida para criar a transformaçao linear
seja T:R3---->R3 onde as bases do nucleo são (1,2,-1),(1,-1,0) encontre T
pensei em chutar um terceiro valor aleatorio tipo(0,0,1) e fazer a combinaçao linear para cair no sistema,mas acredito ser em vão pois não tenho a T(1,2,-1) e T(1,-1,0)
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Fabricio dalla » Dom Nov 15, 2015 20:59
por Fabricio dalla » Dom Nov 15, 2015 20:59
se eu fizer T(1,2,-1)=(0,0,0)
T(1,-1,0)=(0,0,0) ta certo ? vetores que geram a base do nucleo tbm tem que pertecer ao subespaço do nucleo pois t(v)=0 ? posso afirmar isso?
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Qui Nov 19, 2015 16:01
por adauto martins » Qui Nov 19, 2015 16:01

...logo existe
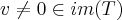
,tal q.
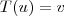
,onde

...
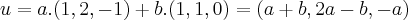
...
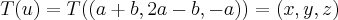
...
como

é unico...teremos...
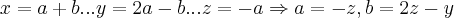
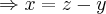
,entao...
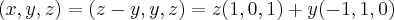
o q. contrairia ,pois
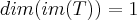
,logo teremos q. ter
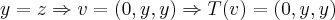
...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Fabricio dalla » Seg Nov 23, 2015 13:38
por Fabricio dalla » Seg Nov 23, 2015 13:38
acho que vc erro o sinal na soma dos vetores na combinaçao linear na parte da coordenada y, mas o mais importante se me explico,estranho é a parte que vc resolve o sistema 3X3 dando uma parte que x=z-y mas enfim,a grande sacada era igualar as variaveis pra atender a condiçao da dimensão da imagem,vlws pela força! obrigado
-
Fabricio dalla
- Colaborador Voluntário

-
- Mensagens: 111
- Registrado em: Sáb Fev 26, 2011 17:50
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Seg Nov 23, 2015 15:49
por adauto martins » Seg Nov 23, 2015 15:49
meu caro fabricio...
é errei na ediçao,mas nao na soluçao...reveja ai...seria
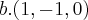
,eu editei
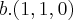
...
aqui temos duas equaçoes e tres incognitas,as quais sao x,y,z todos relacionados com a,b reais quaqueres,entao...
teriamos uma incognita dependo das outras sduas,como a dimensao da imagem igual 1,teriamos q. iguala-las,como visto na soluçao...entao é isso...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Transformação Linear] Nucleo e Imagem, ache a transformaçao
por vualas » Qua Nov 07, 2012 00:37
- 2 Respostas
- 4247 Exibições
- Última mensagem por adauto martins

Qui Dez 15, 2016 11:12
Álgebra Linear
-
- [Algebra Linear] - Composição de transformação Linear
por aligames321 » Ter Dez 04, 2012 23:53
- 1 Respostas
- 10526 Exibições
- Última mensagem por young_jedi

Qua Dez 05, 2012 12:45
Álgebra Linear
-
- Álgebra Linear -Transformação linear- Isomorfismo
por anapaulasql » Ter Jan 27, 2015 22:08
- 1 Respostas
- 11558 Exibições
- Última mensagem por adauto martins

Ter Mar 29, 2016 13:15
Álgebra Linear
-
- [Álgebra Linear] Transformação Linear Idenpotente
por Zubumafu67 » Ter Nov 17, 2020 11:38
- 0 Respostas
- 13597 Exibições
- Última mensagem por Zubumafu67

Ter Nov 17, 2020 11:38
Álgebra Linear
-
- [Álgebra Linear] Transformação linear
por Debby » Dom Mai 27, 2012 12:17
- 2 Respostas
- 9138 Exibições
- Última mensagem por Debby

Dom Mai 27, 2012 20:27
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 ...logo existe
...logo existe 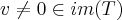 ,tal q.
,tal q.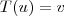 ,onde
,onde  ...
...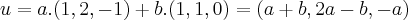 ...
...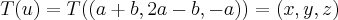 ...
... é unico...teremos...
é unico...teremos...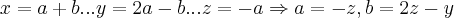
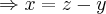 ,entao...
,entao...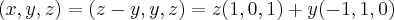 o q. contrairia ,pois
o q. contrairia ,pois 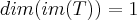 ,logo teremos q. ter
,logo teremos q. ter 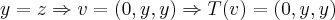 ...
...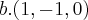 ,eu editei
,eu editei 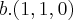 ...
...