Olá, boa tarde a todos.
Um terreno comprado no ano passado foi vendido este
ano por R$ 140.000,00. Sabe-se que a diferença entre o
preço de venda e o preço de compra desse terreno foi
igual a 2/3 do preço de compra. Nessas condições, é cor
reto afirmar que esse terreno foi comprado por
(A) R$ 78.000,00.
(B) R$ 80.000,00
(C) R$ 82.000,00.
(D) R$ 84.000,00.
(E) R$ 92.000,00.
Tentei montar a equação mas não deu certo ... Onde estou errando?
140.000 -x = 2/3.x


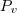 (Preço de venda) ;
(Preço de venda) ;  (Preço de compra)
(Preço de compra)


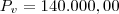 . Para isto, basta substituir o valor de
. Para isto, basta substituir o valor de 

 .
. ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)