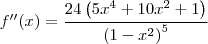por alienpuke » Qui Nov 12, 2015 11:31
por alienpuke » Qui Nov 12, 2015 11:31
Olá, gostaria de saber se essa segunda derivada possui algum ponto de inflexão e se não houver o porquê. Obrigado!
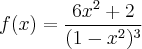
Ps. Tentei igualar a 0 mas nao achei raízes reais. Por esse motivo eu não tenho pontos de inflexão?
-
alienpuke
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 30, 2015 23:23
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Baltuilhe » Sáb Nov 14, 2015 18:14
por Baltuilhe » Sáb Nov 14, 2015 18:14
Boa tarde!!
Calculando a derivada primeira:
![f(x)=\frac{6x^2+2}{\left(1-x^2\right)^3}\\
f'(x)=\frac{\left(6x^2+2\right)'\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[\left(1-x^2\right)^3\right]'}{\left[\left(1-x^2\right)^3\right]^2}\\
f'(x)=\frac{\left(12x\right)\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[3\left(1-x^2\right)^2\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{\left(1-x^2\right)^2\left[\left(12x\right)\cdot\left(1-x^2\right)-\left(6x^2+2\right)\cdot 3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{12x-12x^3+36x^3+12x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x^3+24x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\ f(x)=\frac{6x^2+2}{\left(1-x^2\right)^3}\\
f'(x)=\frac{\left(6x^2+2\right)'\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[\left(1-x^2\right)^3\right]'}{\left[\left(1-x^2\right)^3\right]^2}\\
f'(x)=\frac{\left(12x\right)\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[3\left(1-x^2\right)^2\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{\left(1-x^2\right)^2\left[\left(12x\right)\cdot\left(1-x^2\right)-\left(6x^2+2\right)\cdot 3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{12x-12x^3+36x^3+12x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x^3+24x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\](/latexrender/pictures/dc62af9a2f230df9f4476f0a6d9f2ef3.png)
Agora podemos calcular a derivada segunda:
![f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\
f''(x)=\frac{\left[24x\cdot\left(x^2+1\right)\right]'\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[\left(1-x^2\right)^4\right]'}{\left[\left(1-x^2\right)^4\right]^2}\\
f''(x)=\frac{\left(72x^2+24\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left(3x^2+1\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{\left(1-x^2\right)^3\cdot\left[24\left(3x^2+1\right)\cdot\left(1-x^2\right)-24x\cdot\left(x^2+1\right)\cdot 4\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left[\left(3x^2+1\right)\cdot\left(1-x^2\right)+8x^2\cdot\left(x^2+1\right)\right]}{\left(1-x^2\right)^5}\\
f''(x)=\frac{24\left(3x^2-3x^4+1-x^2+8x^4+8x^2\right)}{\left(1-x^2\right)^5} f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\
f''(x)=\frac{\left[24x\cdot\left(x^2+1\right)\right]'\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[\left(1-x^2\right)^4\right]'}{\left[\left(1-x^2\right)^4\right]^2}\\
f''(x)=\frac{\left(72x^2+24\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left(3x^2+1\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{\left(1-x^2\right)^3\cdot\left[24\left(3x^2+1\right)\cdot\left(1-x^2\right)-24x\cdot\left(x^2+1\right)\cdot 4\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left[\left(3x^2+1\right)\cdot\left(1-x^2\right)+8x^2\cdot\left(x^2+1\right)\right]}{\left(1-x^2\right)^5}\\
f''(x)=\frac{24\left(3x^2-3x^4+1-x^2+8x^4+8x^2\right)}{\left(1-x^2\right)^5}](/latexrender/pictures/f1de3d21d0ccdd131cc205b850a3b75f.png)
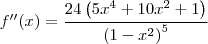
De posse das derivadas consegue resolver o problema, certo?
Calcule as raízes da equação bi-quadrada.
Espero ter ajudado!
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
 por alienpuke » Ter Nov 17, 2015 10:01
por alienpuke » Ter Nov 17, 2015 10:01
Consigo sim, obrigado Baltuilhe!
-
alienpuke
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Qua Set 30, 2015 23:23
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [DERIVADA] Concavidade e pontos de Inflexão
por fabriel » Sex Set 21, 2012 22:56
- 3 Respostas
- 2440 Exibições
- Última mensagem por MarceloFantini

Sáb Set 22, 2012 01:18
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Achar os extremos da função(min/máx/inflexão)
por Fernandobertolaccini » Dom Jul 13, 2014 22:50
- 1 Respostas
- 1783 Exibições
- Última mensagem por e8group

Seg Jul 14, 2014 01:48
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] ajuda para achar quais pontos a função é diferenc
por leohapo » Seg Nov 21, 2016 17:46
- 1 Respostas
- 7499 Exibições
- Última mensagem por adauto martins

Sáb Dez 10, 2016 11:18
Cálculo: Limites, Derivadas e Integrais
-
- Número de pontos de inflexão da seguinte função
por OtavioBonassi » Sáb Jul 16, 2011 14:54
- 1 Respostas
- 1476 Exibições
- Última mensagem por LuizAquino

Sáb Jul 16, 2011 18:04
Cálculo: Limites, Derivadas e Integrais
-
- Derivada: Minimos, máximos e inflexão
por Fernandobertolaccini » Dom Jul 13, 2014 15:35
- 1 Respostas
- 1583 Exibições
- Última mensagem por e8group

Dom Jul 13, 2014 16:01
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
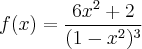

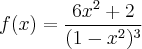

![f(x)=\frac{6x^2+2}{\left(1-x^2\right)^3}\\
f'(x)=\frac{\left(6x^2+2\right)'\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[\left(1-x^2\right)^3\right]'}{\left[\left(1-x^2\right)^3\right]^2}\\
f'(x)=\frac{\left(12x\right)\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[3\left(1-x^2\right)^2\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{\left(1-x^2\right)^2\left[\left(12x\right)\cdot\left(1-x^2\right)-\left(6x^2+2\right)\cdot 3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{12x-12x^3+36x^3+12x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x^3+24x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\ f(x)=\frac{6x^2+2}{\left(1-x^2\right)^3}\\
f'(x)=\frac{\left(6x^2+2\right)'\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[\left(1-x^2\right)^3\right]'}{\left[\left(1-x^2\right)^3\right]^2}\\
f'(x)=\frac{\left(12x\right)\cdot\left(1-x^2\right)^3-\left(6x^2+2\right)\cdot\left[3\left(1-x^2\right)^2\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{\left(1-x^2\right)^2\left[\left(12x\right)\cdot\left(1-x^2\right)-\left(6x^2+2\right)\cdot 3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^6}\\
f'(x)=\frac{12x-12x^3+36x^3+12x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x^3+24x}{\left(1-x^2\right)^4}\\
f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\](/latexrender/pictures/dc62af9a2f230df9f4476f0a6d9f2ef3.png)
![f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\
f''(x)=\frac{\left[24x\cdot\left(x^2+1\right)\right]'\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[\left(1-x^2\right)^4\right]'}{\left[\left(1-x^2\right)^4\right]^2}\\
f''(x)=\frac{\left(72x^2+24\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left(3x^2+1\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{\left(1-x^2\right)^3\cdot\left[24\left(3x^2+1\right)\cdot\left(1-x^2\right)-24x\cdot\left(x^2+1\right)\cdot 4\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left[\left(3x^2+1\right)\cdot\left(1-x^2\right)+8x^2\cdot\left(x^2+1\right)\right]}{\left(1-x^2\right)^5}\\
f''(x)=\frac{24\left(3x^2-3x^4+1-x^2+8x^4+8x^2\right)}{\left(1-x^2\right)^5} f'(x)=\frac{24x\cdot\left(x^2+1\right)}{\left(1-x^2\right)^4}\\
f''(x)=\frac{\left[24x\cdot\left(x^2+1\right)\right]'\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[\left(1-x^2\right)^4\right]'}{\left[\left(1-x^2\right)^4\right]^2}\\
f''(x)=\frac{\left(72x^2+24\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(1-x^2\right)'\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left(3x^2+1\right)\cdot\left(1-x^2\right)^4-24x\cdot\left(x^2+1\right)\cdot\left[4\left(1-x^2\right)^3\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{\left(1-x^2\right)^3\cdot\left[24\left(3x^2+1\right)\cdot\left(1-x^2\right)-24x\cdot\left(x^2+1\right)\cdot 4\cdot\left(-2x\right)\right]}{\left(1-x^2\right)^8}\\
f''(x)=\frac{24\left[\left(3x^2+1\right)\cdot\left(1-x^2\right)+8x^2\cdot\left(x^2+1\right)\right]}{\left(1-x^2\right)^5}\\
f''(x)=\frac{24\left(3x^2-3x^4+1-x^2+8x^4+8x^2\right)}{\left(1-x^2\right)^5}](/latexrender/pictures/f1de3d21d0ccdd131cc205b850a3b75f.png)