Olá anselmojr97!
Está ok, então fico aguardando contato em outra ocasião

Amigo, a ideia é a seguinte:
Vou te explicar como se resolve a letra "a" porque o raciocínio é análogo para as demais questões.
Repare que estamos derivando uma função (parte interna do parêntese) e, essa derivada é feita em relação ao x. A pergunta que nos vem em mente num primeiro momento é: então o que vou fazer com o y?
Bom, se estamos derivando uma função em relação ao x, basta tomarmos o y como constante.
Quando tomamos o y² como constante, nos sobra o produto 20x². sen(x). Neste produto, vamos aplicar as regras usais de derivação junto à Regra do Produto, veja:
y² (40x . sen(x) + cos(x) . 20x²) --> Essa é a resposta do problema.
Com essa dica tente resolver os outros exercícios e esteja à vontade para perguntar caso surgir dúvidas.
Abraço


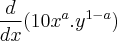 com (0<a<1)
com (0<a<1)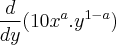 com (0<a<1)
com (0<a<1)





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)