 por Cleyson007 » Qua Nov 04, 2015 14:19
por Cleyson007 » Qua Nov 04, 2015 14:19
Matheusgdp, boa tarde!
Houve um problema na hora de transcrever a função usando o LaTeX. Confirme por favor o que significa o A^² que aparece na função para que eu possa melhor ajudá-lo.
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Matheusgdp » Qua Nov 04, 2015 21:00
por Matheusgdp » Qua Nov 04, 2015 21:00
Boa noite, Cleyson!
Esse A^² realmente não deveria estar aí, mas não consegui retriar ele do LaTex e esqueci de especificar isso. O correto seria sec²x, o restate continua como está, esse A^² não deveria existir aí.
Obrigado pela compreensão! Abraço!
-
Matheusgdp
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Set 16, 2015 03:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em engenharia civil
- Andamento: cursando
 por Cleyson007 » Qui Nov 05, 2015 10:34
por Cleyson007 » Qui Nov 05, 2015 10:34
Matheusgdp, bom dia!
Vamos lá meu amigo.. Estou entrando no fórum agora porque estava envolvido na resolução de algumas listas de exercícios que chegaram por e-mail, mas acredito ainda estar há tempo

Para facilitar o entendimento faça a
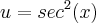
e
![v=\sqrt[]{x} v=\sqrt[]{x}](/latexrender/pictures/ac9c5bcaa4ffcfab429959154047deab.png)
. Dessa forma, temos:

Agora, vamos calcular a

.
A regra de derivação aqui será a seguinte:
Regra da PotênciaO expoente 1/2 passará para frente do parêntese multiplicando o parêntese (agora elevado a -1/2 (ou seja, 1/2 - 1)), multiplicando também a derivada interna do parêntese (u' * v + v' * u --> Regra do Produto).
Seguindo estes passos, obterás como resposta (
em anexo).
Abraço, e bons estudos.
Talvez queira conhecer o meu trabalho, poderei lhe ajudar bastante

Acesse:
viewtopic.php?f=151&t=13614
- Anexos
-
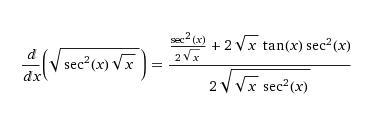
- Derivda - Matheusgdp.png (3.95 KiB) Exibido 3620 vezes
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Matheusgdp » Sex Nov 06, 2015 01:04
por Matheusgdp » Sex Nov 06, 2015 01:04
Muito obrigado, meu dileto! Seguindo seus passos consegui chegar exatamente no resultado anexado, e ainda fiz algumas substituições trigonométricas. Obrigado pela grande ajuda, e por ter apresentado seu trabalho! Irei procurá-lo com toda certeza quando necessário! Um grande abraço!
-
Matheusgdp
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Set 16, 2015 03:22
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em engenharia civil
- Andamento: cursando
 por Cleyson007 » Sex Nov 06, 2015 08:14
por Cleyson007 » Sex Nov 06, 2015 08:14
Está ok meu caro

Fico feliz em poder lhe ajudar.
Aguardo o contato quando necessitar.
Abraço,
Prof° Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivada trigonometrica
por mayara359 » Ter Jun 23, 2015 16:25
- 1 Respostas
- 2512 Exibições
- Última mensagem por Cleyson007

Qua Jun 24, 2015 17:33
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo] Derivada trigonométrica
por ericamila2 » Sáb Set 24, 2011 22:39
- 1 Respostas
- 1420 Exibições
- Última mensagem por LuizAquino

Sáb Set 24, 2011 23:14
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de Função Trigonométrica.
por Sobreira » Dom Dez 02, 2012 14:17
- 2 Respostas
- 3539 Exibições
- Última mensagem por MarceloFantini

Seg Dez 03, 2012 00:08
Cálculo: Limites, Derivadas e Integrais
-
- [AJUDA] Duvida de derivada trigonométrica
por Erick Johnny » Ter Mai 29, 2012 11:01
- 3 Respostas
- 2481 Exibições
- Última mensagem por LuizAquino

Ter Mai 29, 2012 13:37
Cálculo: Limites, Derivadas e Integrais
-
- Derivada de uma função trigonométrica [Resposta impossível]
por Matheus Lacombe O » Dom Dez 02, 2012 13:57
- 3 Respostas
- 3113 Exibições
- Última mensagem por DanielFerreira

Dom Dez 02, 2012 17:51
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![f(x)=\,\sqrt[]{sec²x\,\,\sqrt[]{x}} f(x)=\,\sqrt[]{sec²x\,\,\sqrt[]{x}}](/latexrender/pictures/5352b27ef006f14684c6ba315c9374ba.png)


![f(x)=\,\sqrt[]{sec²x\,\,\sqrt[]{x}} f(x)=\,\sqrt[]{sec²x\,\,\sqrt[]{x}}](/latexrender/pictures/5352b27ef006f14684c6ba315c9374ba.png)




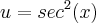 e
e ![v=\sqrt[]{x} v=\sqrt[]{x}](/latexrender/pictures/ac9c5bcaa4ffcfab429959154047deab.png) . Dessa forma, temos:
. Dessa forma, temos:
 .
. Acesse: viewtopic.php?f=151&t=13614
Acesse: viewtopic.php?f=151&t=13614





 , avisa que eu resolvo.
, avisa que eu resolvo.

