FGE0160
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por 9oito » Qua Out 21, 2015 17:25
por 9oito » Qua Out 21, 2015 17:25
Me ajudem!!
Você não está autorizado a ver ou baixar esse anexo.
-
9oito
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qua Out 21, 2015 17:16
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Ensino Médio
- Andamento: cursando
 por DanielFerreira » Sáb Out 31, 2015 20:00
por DanielFerreira » Sáb Out 31, 2015 20:00
Olá! Seja bem-vindo(a)!
Repare que os módulos dos vetores

,
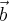
e
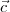
correspondem à diagonal de um retângulo cujos lados valem 1 e 2 centímetros.
Calculando tais diagonais concluirá que todas valem
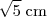
.
Isto posto, temos que:
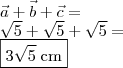
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Óptica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [G.A] Soma ponto c/ vetor
por ViniciusAlmeida » Qui Abr 23, 2015 16:49
- 0 Respostas
- 1352 Exibições
- Última mensagem por ViniciusAlmeida

Qui Abr 23, 2015 16:49
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4889 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2081 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- Integral da soma/Soma das Integrais.
por Sobreira » Ter Abr 30, 2013 17:41
- 0 Respostas
- 2094 Exibições
- Última mensagem por Sobreira

Ter Abr 30, 2013 17:41
Cálculo: Limites, Derivadas e Integrais
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 8383 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ,
, 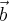 e
e 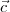 correspondem à diagonal de um retângulo cujos lados valem 1 e 2 centímetros.
correspondem à diagonal de um retângulo cujos lados valem 1 e 2 centímetros.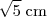 .
.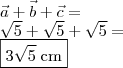

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.