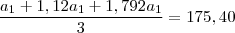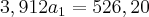por parrala » Dom Out 04, 2015 19:13
por parrala » Dom Out 04, 2015 19:13
Olá boa tarde
Qual a formula matemática para encontrar a1 em uma progressão de 3 termos com razão variável conhecendo somente a média dos 3 termos e as razões entre os termos
Exemplo:
Sabendo que a média de a1,a2 e a3 é igual a 175,40 e que a razão de a1 para a2 é 1,12 e a razão de a2 para a3 é 1,6 qual é o valor de a1?
((a1+a2+a3)/3) = 175,40
q1=1,12
q2=1,6
a1= ??
Desde já muito grato
Ronqui
-
parrala
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 04, 2015 19:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia
- Andamento: formado
 por nakagumahissao » Dom Out 04, 2015 21:36
por nakagumahissao » Dom Out 04, 2015 21:36
parrala,
Não existe uma fórmula só para se resolver problemas como estes. Você precisará raciocinar adequadamente para cada caso. No caso em questão, se a média é:
![\frac{{a}_{1} + {a}_{2} + {a}_{3}}{3 } = 175,40\;\;\;\;\;[1] \frac{{a}_{1} + {a}_{2} + {a}_{3}}{3 } = 175,40\;\;\;\;\;[1]](/latexrender/pictures/77195257766cad70d9faa234e5b34ffd.png)
e as razões são:
q1=1,12
q2=1,6
e se considerarmos por hipótese que você esteja falando em uma sequência do tipo:

![{a}_{2} = {a}_{1} + {q}_{1} \;\;\;[2] {a}_{2} = {a}_{1} + {q}_{1} \;\;\;[2]](/latexrender/pictures/9255f954741d732787bf156a3cc1eed9.png)
![{a}_{3} = {a}_{2} + {q}_{2}\;\;\;\;\[3] {a}_{3} = {a}_{2} + {q}_{2}\;\;\;\;\[3]](/latexrender/pictures/83d529f39f6ef043af6de250a2479a10.png)
então, vamos tentar escrever a equação [1] somente em termos de uma só variável. Escolherei a1. Então, de [3], uitlizando [2], tem-se que:
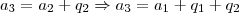
Trocando q1 e q2 pelos seus respectivos valores teremos:
![{a}_{3} = {a}_{1} + 1,12 + 1,6 = {a}_{1} + 2,72\;\;\;\;\;[4] {a}_{3} = {a}_{1} + 1,12 + 1,6 = {a}_{1} + 2,72\;\;\;\;\;[4]](/latexrender/pictures/b5e4188f71e2a995343df6bfdff3a1b2.png)
Como [2] já se encontra em função de a1, vamos agora substituir [2] e [4] em [1]:
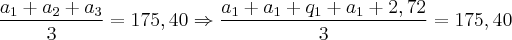
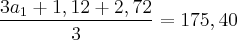

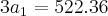
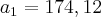
Com este valor e utilizando nas equações [2] e [4], obtemos os outros valores desejados:

e

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
 por parrala » Dom Out 04, 2015 21:51
por parrala » Dom Out 04, 2015 21:51
Boa noite nakagumahissao , estou falando em uma sequência do tipo:
a1 = a1
a2 = a1 X q1
a3 = a2 X q2
Obrigado
-
parrala
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Out 04, 2015 19:03
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia
- Andamento: formado
 por nakagumahissao » Seg Out 05, 2015 01:22
por nakagumahissao » Seg Out 05, 2015 01:22
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- P.G. (Encontrar os termos)
por Rafael16 » Qua Jul 18, 2012 23:15
- 1 Respostas
- 2500 Exibições
- Última mensagem por Russman

Qui Jul 19, 2012 00:02
Progressões
-
- [ PA ] Encontrar termos
por GrazielaSilva » Qui Out 04, 2012 12:42
- 2 Respostas
- 3099 Exibições
- Última mensagem por GrazielaSilva

Sex Out 05, 2012 01:22
Progressões
-
- [ PA ] Encontrar termos
por GrazielaSilva » Qui Out 11, 2012 12:25
- 1 Respostas
- 1668 Exibições
- Última mensagem por young_jedi

Qui Out 11, 2012 14:08
Progressões
-
- [Progressões] Encontrar os primeiros termos
por GrazielaSilva » Sex Set 28, 2012 11:28
- 2 Respostas
- 12982 Exibições
- Última mensagem por Yokotoyota

Qui Fev 04, 2016 03:09
Progressões
-
- Produto dos Termos da Progressão Geométrica
por petras » Ter Nov 22, 2016 20:33
- 0 Respostas
- 6654 Exibições
- Última mensagem por petras

Ter Nov 22, 2016 20:33
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


![\frac{{a}_{1} + {a}_{2} + {a}_{3}}{3 } = 175,40\;\;\;\;\;[1] \frac{{a}_{1} + {a}_{2} + {a}_{3}}{3 } = 175,40\;\;\;\;\;[1]](/latexrender/pictures/77195257766cad70d9faa234e5b34ffd.png)

![{a}_{2} = {a}_{1} + {q}_{1} \;\;\;[2] {a}_{2} = {a}_{1} + {q}_{1} \;\;\;[2]](/latexrender/pictures/9255f954741d732787bf156a3cc1eed9.png)
![{a}_{3} = {a}_{2} + {q}_{2}\;\;\;\;\[3] {a}_{3} = {a}_{2} + {q}_{2}\;\;\;\;\[3]](/latexrender/pictures/83d529f39f6ef043af6de250a2479a10.png)
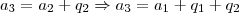
![{a}_{3} = {a}_{1} + 1,12 + 1,6 = {a}_{1} + 2,72\;\;\;\;\;[4] {a}_{3} = {a}_{1} + 1,12 + 1,6 = {a}_{1} + 2,72\;\;\;\;\;[4]](/latexrender/pictures/b5e4188f71e2a995343df6bfdff3a1b2.png)
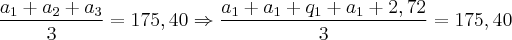
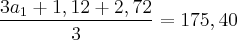

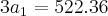
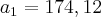



![\frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}= 175,40\;\;\; [1] \frac{{a}_{1}+{a}_{2}+{a}_{3}}{3}= 175,40\;\;\; [1]](/latexrender/pictures/ce15f29921df86e6b0add9dca881364a.png)
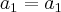
![{a}_{2}={a}_{1}{q}_{1}={a}_{1}1, 12\:\:\; [2] {a}_{2}={a}_{1}{q}_{1}={a}_{1}1, 12\:\:\; [2]](/latexrender/pictures/7e2cd610848f4d19cee619068cf51276.png)
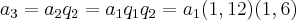
![{a}_{3}={a}_{1}(1,792) \;\;\; [3] {a}_{3}={a}_{1}(1,792) \;\;\; [3]](/latexrender/pictures/a8902c6f82c876088c74e78c014015ea.png)