RJ1572 escreveu:Considere todos os números de 4 algarismos distintos, formados com os dígitos 1,2,3,4,5,6,7,8 e 9. Quantos destes são ímpares e maiores que 3000?
A resposta é 1302, mas não estpou conseguindo chegar a essa resposta.
Boa tarde.
Problemas assim faça como Jack, vá por partes,
rs...Primeiramente verifique o total de números ímpares de 4 algarismos distintos:Para isso temos apenas
cinco opções para o algarismo da unidade (1,3,5,7 e 9);
oito opções para o algarismo da dezena;
sete opções para o algarismo da centena; e
seis opções para o algarismo da unidade de milhar. Multiplicando os valores
sublinhados:
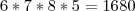
Agora vamos retirar desses 1680, os algarismos menores de 3000, da seguinte forma:
Números de 4 algarismos que iniciem com o algarismo 1: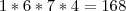
(modo de opções igual fiz anteriormente)
Note que como o primeiro algarismo é o 1 (número ímpar), resta apenas 4 opções para o algarismo da unidade (3,5,7 e 9).
Números de 4 algarismos que iniciem com o algarismo 2: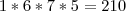
(modo de opções igual fiz anteriormente)
Note que como o primeiro algarismo é o 2 (número par), resta ainda 5 opções para o algarismo da unidade (1,3,5,7 e 9).
Total de números ímpares de 4 algarismos distintos menores que 3000: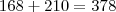 Números de 4 algarismos distintos, ímpares e maiores que 3000:
Números de 4 algarismos distintos, ímpares e maiores que 3000: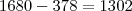
Acho que está bem detalhado. Mas se não entender alguma passagem, avise!




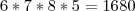
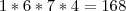 (modo de opções igual fiz anteriormente)
(modo de opções igual fiz anteriormente)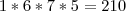 (modo de opções igual fiz anteriormente)
(modo de opções igual fiz anteriormente)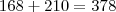
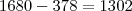



 .
.
 :
: