Estou com uma dúvida nessas 3 questões:
1°) Sejam f um escalar e F um campo vetorial quaisquer. Se existem as derivadas parciais provar: div(f F) = f [ div(F)] + [ grad(f)] * F
2°)Se r(vetor)= xi + yj + zk é o chamado vetor posição, provar:
a) div(r) = 3
b) rot(r) = 0
c)Nabla II r II = r / |r|
3°) define-se nabla^2 como operador Laplaciano.
a) definir nabla^2 através de derivadas parciais;
b) se f e g são funções escalares dotadas de derivadas parciais segundas, provar :
nabla*(nabla f )= nabla^2 f
Segue o gabarito com as respostas :
1°)div (F) = f [div (F)] + [ grad (f) ] * F...é verdadeira.
2°) a) div (r) =3 ; b) rot (r) = 0 ; c) Nabla |r|= r / |r|...verdadeira
3°)verdadeira..
obs: Estou tendo muita dificuldade de com esses exercícios. seria possível mostrar o passo a passo até o resultado?


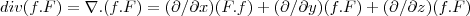 ..MEU EDITOR NAO ESTA FUNCIONANDO AQUI,MAS VAMOS LA NO JEITO Q. DER...
..MEU EDITOR NAO ESTA FUNCIONANDO AQUI,MAS VAMOS LA NO JEITO Q. DER...


 , avisa que eu resolvo.
, avisa que eu resolvo.

