


 tem estrutura de espaço vetorial sobre um corpo
tem estrutura de espaço vetorial sobre um corpo  e que um conjunto
e que um conjunto  tem estrutura de espaço vetorial sobre um corpo
tem estrutura de espaço vetorial sobre um corpo  . Se qualquer subconjunto de
. Se qualquer subconjunto de  não tiver estrutura de espaço vetorial sobre o corpo
não tiver estrutura de espaço vetorial sobre o corpo  , então qualquer aplicação
, então qualquer aplicação  não satisfaz :
não satisfaz : 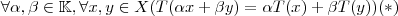 .
.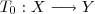 , fosse uma aplicação satisfazendo tal propriedade , nesse caso o subconjunto
, fosse uma aplicação satisfazendo tal propriedade , nesse caso o subconjunto  é um espaço vetorial sobre
é um espaço vetorial sobre  . (Verifique !) ) .
. (Verifique !) ) .  implica que
implica que  . Ora ,nesse caso caso temos que ter uma aplicação bem definida
. Ora ,nesse caso caso temos que ter uma aplicação bem definida 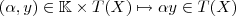 . Do contrário o segundo membro de (*) não faz sentido . Mas se Y não tiver estrutura de esp. vetorial sobre o mesmo corpo que o espaço de saida , o que garanti que pelo menos a aplicação acima pode ser bem definida ?x]
. Do contrário o segundo membro de (*) não faz sentido . Mas se Y não tiver estrutura de esp. vetorial sobre o mesmo corpo que o espaço de saida , o que garanti que pelo menos a aplicação acima pode ser bem definida ?x] 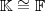 ? Neste
? Neste 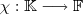 .
.  para X , e escolha de forma arbitrária n vetores em Y , digamos
para X , e escolha de forma arbitrária n vetores em Y , digamos  .
.  que se exprime unicamente como
que se exprime unicamente como  ; a correspondência
; a correspondência 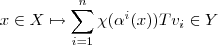 define uma aplicação
define uma aplicação  que satisfaz
que satisfaz 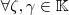
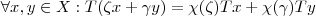
 for subcorpo de
for subcorpo de  , basta tomar
, basta tomar  como a inclusão
como a inclusão 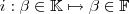 que é claramente um homomorfismo . Nesse caso , vale
que é claramente um homomorfismo . Nesse caso , vale 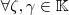
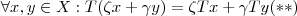 .Para evitar 'complicações' já refinamos e pedimos algo mais : Pedimos que ambos espaços vetoriais sejam sobre o mesmo corpo . Nota tbm que os exemplos mais interessantes em estudo são de espaços vetoriais sobre R ou C , principalmente os normados ...
.Para evitar 'complicações' já refinamos e pedimos algo mais : Pedimos que ambos espaços vetoriais sejam sobre o mesmo corpo . Nota tbm que os exemplos mais interessantes em estudo são de espaços vetoriais sobre R ou C , principalmente os normados ...

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes





