Suponha f definida e contínua nos Reais e que f (x) = 0 para todo x racional. Prove que f (x)=0,
para todo x real.(Sugestão:use o teorema da conservação do sinal).



 para designar
para designar 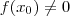 . Só para fixar ideias , assuma
. Só para fixar ideias , assuma 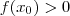 (0 outro caso é inteiramente análogo ) . Como f é contínua , então vale a " conservação do sinal " , e assim teremos , para algum
(0 outro caso é inteiramente análogo ) . Como f é contínua , então vale a " conservação do sinal " , e assim teremos , para algum 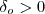 ,
, 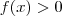 para todo
para todo 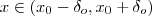 .Mas , pela densidade dos racionais em
.Mas , pela densidade dos racionais em  , temos
, temos 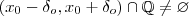 , o que implica
, o que implica  p/ algum x racional que es uma contradição !
p/ algum x racional que es uma contradição !  . Fixe
. Fixe 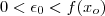 . Dado qualquer
. Dado qualquer 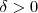 , por densidade , o intervalo aberto
, por densidade , o intervalo aberto 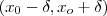 contém números racionais .Assim , temos um racional
contém números racionais .Assim , temos um racional 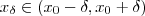 , mas
, mas 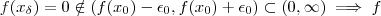 descontínua em
descontínua em  (Contradição !)
(Contradição !)  )
) 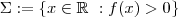 é aberto em
é aberto em  , pois tal conjunto é simplesmente a preimagem do intervalo aberto
, pois tal conjunto é simplesmente a preimagem do intervalo aberto  pela aplicação contínua
pela aplicação contínua  . Ora , então só pode ser
. Ora , então só pode ser 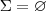 , do contrário , dado
, do contrário , dado 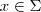 , podemos obter
, podemos obter  tal que
tal que 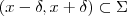 , uma contradição ! (Pois
, uma contradição ! (Pois  é denso em
é denso em  , e isto implica
, e isto implica 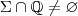 )x]
)x] 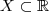 , tem-se
, tem-se 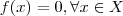 então f se anula em todos os pontos do fecho de X
então f se anula em todos os pontos do fecho de X 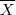 . Fixe
. Fixe 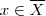 . Qualquer intervalo aberto contendo x tem interseção não vazia com X (usando a caracterização para o fecho ) . Nota que ou
. Qualquer intervalo aberto contendo x tem interseção não vazia com X (usando a caracterização para o fecho ) . Nota que ou 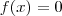 ou
ou 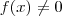 . Se
. Se  fosse
fosse  , tomando
, tomando 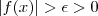 , o intervalo aberto
, o intervalo aberto 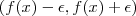 não conteria o zero . Mas , para qualquer
não conteria o zero . Mas , para qualquer  ,
, 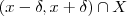 é não vazio (pois x está no fecho de X ) .Assim , dado
é não vazio (pois x está no fecho de X ) .Assim , dado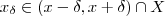 temos
temos 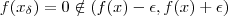 o que implica f descontínua em x . Contradição ! Portanto ,
o que implica f descontínua em x . Contradição ! Portanto , 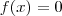 .Como x é arbitrário , obtemos
.Como x é arbitrário , obtemos 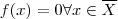 .
. 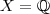 ) , então f se anula em todos os pontos de
) , então f se anula em todos os pontos de 
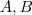 ...
... 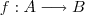 , podemos definir as seguintes funções
, podemos definir as seguintes funções 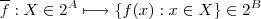 e
e 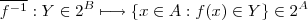 .
. 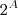 denote a coleção de todos os subconjuntos de A .
denote a coleção de todos os subconjuntos de A . 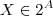 (que é a mesma coisa dizer
(que é a mesma coisa dizer 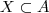 ) , chamamos o conjunto
) , chamamos o conjunto 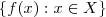 de imagem direta de X por f e por abuso de notação simplesmente denotamos por
de imagem direta de X por f e por abuso de notação simplesmente denotamos por  (em particular quando X = A , tem o conjunto imagem da função f )
(em particular quando X = A , tem o conjunto imagem da função f ) 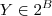 , chamamos o conjunto
, chamamos o conjunto 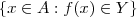 de preimagem (ou imagem inversa ) e denotamos por abuso de notação
de preimagem (ou imagem inversa ) e denotamos por abuso de notação 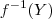 (Não é imagem direta de Y pela função inversa , cuidado ! Nem se sabe se f admite uma inversa )
(Não é imagem direta de Y pela função inversa , cuidado ! Nem se sabe se f admite uma inversa )
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.