 por nakagumahissao » Ter Ago 18, 2015 12:23
por nakagumahissao » Ter Ago 18, 2015 12:23
D4rwin,
A forma de raciocionar é bem simples. Eu faço da seguinte forma (outros podem fazer diferentemente). Eu vou lendo a questão e quando me deparo com alguma informação importante, tento transformar o que lí em uma equação, fórmula, designação de variável, etc. e depois de ler umas duas ou três vezes para ter certeza de que minhas fórmulas e números representam mesmo o que eu estou lendo, passo para a resolução do problema, buscando aquilo que me foi pedido na questão.
Vou explicar melhor. No caso do problema que passou:
A "fórmula 95" dá direito de um trabalhador se aposentar quando a soma de sua idade (em anos) e seu tempo de serviço (em anos) resulte em 95. Considere que uma pessoa comece a trabalhar com 22 anos. Com que idade ela se aposentará, de acordo com essa fórmula?
Nesta parte, você deveria começar então a se questionar. "Como posso colocar isso em uma fórmula ou expressar esta informação com números?". Pensando desta forma, vamos colocar isso no papel: Ele diz, esta fórmula 95 dá direito de um trabalhador se aposentar quando a "SOMA"... Opa! Temos que somar alguma coisa e para somarmos alguma coisa, precisamos de no mínimo 2 coisas! Então nos perguntamos: Vamos somar o que? Precisamos de 2 coisas no mínimo!
Então continuamos a ler: "SOMA DE SUA IDADE... E SEU TEMPO DE SERVIÇO" (Que estão em anos!), então, precisamos criar duas "VARIÁVEIS" para representar cada coisa. Quando eu digo representar, quero dizer que IDADE e TEMPO DE SERVIÇO podem ser representados por uma letra do nosso alfabeto. Eles são como atores de novela, representando outra pessoa. Então, para que a gente possa somar essas duas coisas, precisamos abreviar nosso trabalho e criando duas variáveis (uma para cada coisa), facilitará nossas contas. Assim, começamos "dando nomes aos bois", da seguinte maneira - repare no texto:
"Sejam I a Idade e T o Tempo de Serviço..."
Agora, para somar alguma coisa, precisamos colocar este resultado em algum lugar. Precisamos de um variável também para o resultado desta soma. Então vamos criar mais uma variável da seguinte maneira:
"Sejam S a soma da Idade com o Tempo de Serviço, I a Idade e T o Tempo de Serviço..."
Agora podemos prosseguir e mostrar nossa equação:
"Sejam S a soma da Idade com o Tempo de Serviço, I a Idade e T o Tempo de Serviço, então: S = I + T".
Fazendo S = I + T é muito mais simples do que:
SOMA DAS IDADE COM O TEMPO DE SERVIÇO = IDADE + TEMPO DE SERVIÇO
não é mesmo? Por isso criamos as variáveis para facilitar.
Retornando ao nosso texto, vamos prosseguir:
A "fórmula 95" dá direito de um trabalhador se aposentar quando a soma de sua idade (em anos) e seu tempo de serviço (em anos) resulte em 95. Considere que uma pessoa comece a trabalhar com 22 anos. Com que idade ela se aposentará, de acordo com essa fórmula?
Veja que ele diz que a soma da idade e o tempo de serviço deverão atingir 95 para poder se aposentar. Assim, como já temos a fórmula da soma S = I + T, podemos dizer que o "S", que e a soma da idade e do tempo de serviço deverão ser 95 para poder se aposentar. Isso que dizer o que? Que S TEM que ser 95 para se aposentar! Logo,
S = 95
Essa é a condição para o trabalhador ganhar a aposentaria nessa fórmula 95. Assim terminamos de identificar as partes "MATEMÁTICAS" desta frase. Vamos sumarizar abaixo o que já temos:
S = I + T
S = 95
Agora vamos prosseguir e identificar as partes "MATEMÁTICAS" que existem no restante do parágrafo do enunciado:
"Considere que uma pessoa comece a trabalhar com 22 anos[/color]. Com que idade ela se aposentará, de acordo com essa fórmula?"
Nesta parte em azul, ele diz que o trabalhador começa a trabalhar com 22 anos. Isso não é uma suposição, é uma afirmação, é uma certeza neste caso em particular. Assim, você teria que pensar. 22 anos tem a ver com o I ou com T, ou seja, com a Idade ou com o Tempo de Serviço (os dois são em anos)! Veja bem, "o trabalhador começa a trabalhar com 22 anos" e colocado de outra forma, ficaria: "O trabalhador começa a trabalhr com a IDADE de 22 anos", não é mesmo? Pois não teria sentido dizer que o tempo de serviço dele começou com 22 anos! A pessoa começa seu tempo de serviço no Tempo = Zero!. Portanto, esta frase indica que a Idade para o cálculo deverá ser 22 anos! Escrevendo isso na forma "MATEMÁTICA" ficaria:
I = 22
Até aqui, tudo bem? Alguma dúvida? Me pergunte se necessário!
Vamos colocar agora tudo que encontramos:
Sabemos que S = I + T, que S = 95 e que I = 22.
O restante da frase diz:
"Considere que uma pessoa comece a trabalhar com 22 anos. Com que idade ela se aposentará, de acordo com essa fórmula?"
- Com que idade ela se aposentará, de acordo com essa fórmula? - É uma PERGUNTA (tem ponto de interrogação!). Assim, esta é a parte que precisamos guardar em mente e resolver o problema de forma a encontar o que se está sendo pedido, ou seja QUANDO ou QUANTO TEMPO ela terá que trabalhar para se aposentar?
Veja, você já tem DOIS valores da fórmula: S = 95 e I = 22 e sua fórmula têm 3 (três) variáveis que são S, I e T. Sendo que você tem duas das variáveis e somente uma não tem, logo, só pode ser esta variável que precisa ser calculada. O que sobra é o T e o T é o Tempo que o trabalhador terá que trabalhar para se aposentar, não é mesmo? Releia o momento em que criamos estas variáveis acima se necessário ou se esqueceu do raciocínio!
Assim, vamos agora para a parte MATEMÁTICA da coisa. Vamos primeiramente colocar a fórmula que determinamos:
S = I + T
Depois, ir trocando variável por variável com os valores que nós JÁ TEMOS (S = 95 e I = 22). Assim:
S = I + T => 95 = 22 + T
Aí é só resolver a equação. Trocando tudo de lados: T + 22 = 95. Passando o 22 para a direita, teremos: T = 95 - 22 e finalmente, teremos a resposta: T = 73
Voltando de novo ao enunciado, vemos que ele diz que T e I estão em anos, portanto, S também terá que ser em anos. A pergunta que deve se fazer agora é: Esta resposta é em Anos, Meses, Dias, Anos-luz, Segundos, Horas, Pascal, Newtons, ... O que? Isso! - É em ANOS!
Assim, terminamos então de resolver o problema com a seguinte resposta - O tempo para que este indivíduo que começou a trabalhar com 22 anos precisa para se aposentar será de 73 anos.
A forma com que deverá tratar todos os problemas é bem parecida. É claro que a dificuldade e a quantidade de respostas de cada problema varia. Você vai encontrar muitos cujo entendimento é simples, outras médias e outras muito complicadas em que alguns você conseguirá resolver facilmente e outras nem tanto e em muitas, nem mesmo saberá como resolver. Assim, o conselho que dou é: aprenda tudo o que puder da teoria e pratique muito nos exercícios e procure praticar sempre para não esquecer pois a matemática se constrói por degraus e o que você aprende hoje será usado amanhã e quem sabe futuramente, no seu trabalho como cientista, engenheiro, físico, químico, arquiteto, Analista de Sistemas, Programador, Matemático, Biólogo, Psicólogo, etc.! Tudo que você aprendeu pode facilitar em muito a transformação das frases que lê nos problemas para a "LINGUAGEM MATEMÁTICA" e principalmente, te dar idéias de como resolver os problemas que aparecerão tanto em forma escrita, como também no seu dia-a-dia.
Lembre-se também que ninguém é infalível. Sempre há várias questões que não iremos conseguir resolver e que outra pessoa pode ajudar a resolver por enxergar o problema de outra forma. Assim, não espere que você venha a conseguir resolver TODOS os problemas. Só gênios conseguiriam, talvez! - A quantidade de problemas que conseguirá resolver está intimamente ligada à quantidade de conhecimento que for adquirindo durante sua vida em TODAS as áreas do conhecimento (uma está ligada à outra de alguma forma)
Espero que tenha ajudado.
Sandro
Editado pela última vez por
nakagumahissao em Ter Ago 18, 2015 22:58, em um total de 1 vez.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali



![T = I - 22 \;\;\;\;\;[1] T = I - 22 \;\;\;\;\;[1]](/latexrender/pictures/12c7195bf5202fee2bb5311f06ab5f81.png)



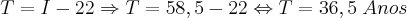


 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.