Elvis,
Respondedo suas perguntas e fazendo algumas observações:
Não sei em que nível escolar está neste momento, mas independente disso, a resposta da primeira pergunta é: sim. No limite superior deverá ser a variável sim, pelo menos até onde estudei (Matemática, nível universitário)
Agora, existem duas respostas para a sua segunda pergunta:
Como eu poderia calcular a integral da função g?
1) Poderíamos fazer simplesmente:
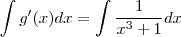
E se o intervalo (1,h) fosse dado:

2) Agora, para realmente calcularmos esta integral, fazemos uso de algumas técnicas de integração e por isso, dependerá muito do seu grau de conhecimento de Cálculo I. Se você está terminando ou já está se aproximando do final do curso de Cálculo I, então você já deve ter visto estas técnicas. Se não viu, você somente terá o básico da integração ou seja, as formas mais básicas possíveis de funções para que sejam integradas como exercícios.
Vou resolver essa para você ver:

Esta integral pode ser resolvida por Frações Parciais. Neste caso, para sabermos o tipo de fração parcial a ser utilizada, precisaremos primeiramente fatorar o denominador. Por tentativa e erro, sabemos que uma das raízes do denominador é x = -1. assim, dividindo-se
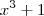
por

, teremos:
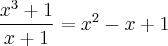
Logo:
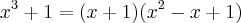
Completando o quadrado em

temos:
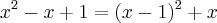
Assim, a fração parcial que precisaremos encontrar será:
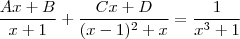
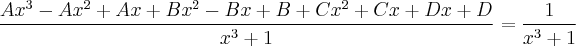
Fatorando...
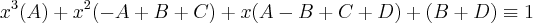
![A = 0 ;\;\;\;\;[1] A = 0 ;\;\;\;\;[1]](/latexrender/pictures/4c8fb4e5a4902dd9f3abf4a0888eb2ef.png)
![A - B + C + D = 0 \;\;\;\;\; [2] A - B + C + D = 0 \;\;\;\;\; [2]](/latexrender/pictures/7446e5abfd3f534fc4a54cabde699199.png)
![-A + B + C = 0 \;\;\;\;\; [3] -A + B + C = 0 \;\;\;\;\; [3]](/latexrender/pictures/cb296d6eae3acf77b20813c009fb817a.png)
![B + D =1 \;\;\;\;\;[4] B + D =1 \;\;\;\;\;[4]](/latexrender/pictures/5711a3e0ae67c5afea8b0031a3ae4db0.png)
Resolvendo este sistema de equações encontraremos:


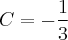
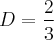
Assim:
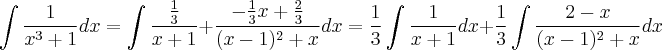
Solução da Primeira Integral:
![\frac{1}{3}\int \frac{1}{x + 1} dx = \frac{1}{3} \ln |x+1| + c_{1} \;\;\;\;\; [5] \frac{1}{3}\int \frac{1}{x + 1} dx = \frac{1}{3} \ln |x+1| + c_{1} \;\;\;\;\; [5]](/latexrender/pictures/23c0efbfe1bdec61979300dc3bae36eb.png)
Segunda Integal:
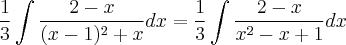
Podemos reescrever:
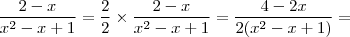
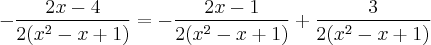
Integrando, tem-se:


![=-\frac{1}{6}\int \frac{2x - 1}{x^2 - x + 1}dx + \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\;\;[6] =-\frac{1}{6}\int \frac{2x - 1}{x^2 - x + 1}dx + \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\;\;[6]](/latexrender/pictures/b42d4bcbb05714f088cb81ef6d466930.png)
Resolvendo a primeira integral de [6], tem-se que:



![= -\frac{1}{6} \ln |x^2 - x + 1| + c_{2} \;\;\;\;\; [7] = -\frac{1}{6} \ln |x^2 - x + 1| + c_{2} \;\;\;\;\; [7]](/latexrender/pictures/dd86ecb758e06b42d81db1f85d3a08cf.png)
Resolvendo a segunda integram em [6], tem-se que:
![\frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\; [8] \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\; [8]](/latexrender/pictures/320eb1c3ce5d24af85e063ca12078043.png)
Mas:
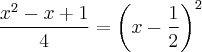
Então, uma boa escolha para substituição será:
![u = x - \frac{1}{2} \Rightarrow du = dx \;\;\;\; [9] u = x - \frac{1}{2} \Rightarrow du = dx \;\;\;\; [9]](/latexrender/pictures/d29990536b80197d4839453fef30f708.png)
Usando [9] em [8], tem-se:
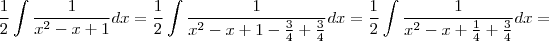

![= \frac{1}{2}\int \frac{4}{4u^{2} + 3} dx \;\;\;\;\;[10] = \frac{1}{2}\int \frac{4}{4u^{2} + 3} dx \;\;\;\;\;[10]](/latexrender/pictures/5c1fdfc811ddd7445f490e7ebdac5f0c.png)
Vamos substituir em [10] por:
![u = \frac{\sqrt{3}}{2}\tan \theta \Rightarrow du = \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta \;\;\;\;\; [11] u = \frac{\sqrt{3}}{2}\tan \theta \Rightarrow du = \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta \;\;\;\;\; [11]](/latexrender/pictures/84da24cf05eeda82c8ffb829778d64ee.png)
![= \frac{1}{2}\int \frac{4}{3\left[\left( \frac{\sqrt{3}}{2}\tan \theta \right)^2 + \frac{3}{4} \right]} \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta = \int \frac{\sqrt{3}\sec^{2} \theta }{\frac{9}{4}\left( \tan^{2} + 1 \right)} d\theta = = \frac{1}{2}\int \frac{4}{3\left[\left( \frac{\sqrt{3}}{2}\tan \theta \right)^2 + \frac{3}{4} \right]} \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta = \int \frac{\sqrt{3}\sec^{2} \theta }{\frac{9}{4}\left( \tan^{2} + 1 \right)} d\theta =](/latexrender/pictures/97221aed7cb73ee0aec5d011b5087d83.png)
![\int \frac{4\sqrt{3}\sec^{2} \theta }{9\sec^{2}} d\theta = \frac{4\sqrt{3}}{9} \theta + c_{3} \;\;\;\;\; [12] \int \frac{4\sqrt{3}\sec^{2} \theta }{9\sec^{2}} d\theta = \frac{4\sqrt{3}}{9} \theta + c_{3} \;\;\;\;\; [12]](/latexrender/pictures/1dd4528e9d58237accb50be0c02dc467.png)
Revertendo-se usando [11] em [12] tem-se:

Aplicando-se [9]:
![\Rightarrow \tan \theta = \frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \Rightarrow \theta = \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] \Rightarrow \tan \theta = \frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \Rightarrow \theta = \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right]](/latexrender/pictures/4e999e0fe33bcf95657b1808839fce99.png)
Finalmente, substituindo-se este resultado em [12] temos:
![= \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + c_{3} \;\;\;\;\; [13] = \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + c_{3} \;\;\;\;\; [13]](/latexrender/pictures/c33b5b2fc9fd861ee55e722391cd9581.png)
Juntando-se finalmente todos os resultados obtidos de cada integral, temos a resposta final:

![= \frac{1}{3} \ln |x+1| - \frac{1}{6} \ln |x^2 - x + 1| + \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + C = \frac{1}{3} \ln |x+1| - \frac{1}{6} \ln |x^2 - x + 1| + \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + C](/latexrender/pictures/bca70d7038848ea24448e32f72d0e507.png)
Como pode observar, esta integral é bem complexa e a resolução de integrais depende do seu conhecimento de várias técnicas de integração ensinadas no Cálculo I: Substituição, Frações Parciais, Substituição Trigonométrica, Integração por partes, Tabelas de Integração, Fórmula de Taylor, Integração Numérica, etc.

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali




![\frac{d}{dx}\left[\int_{a}^{x} f(t)dt \right] = f(x) \frac{d}{dx}\left[\int_{a}^{x} f(t)dt \right] = f(x)](/latexrender/pictures/89bb0cf51ba3eada5ce136516f378971.png)
![\frac{d}{dx}\left[\int_{a}^{x} f(t)dt \right] = f(x) \frac{d}{dx}\left[\int_{a}^{x} f(t)dt \right] = f(x)](/latexrender/pictures/89bb0cf51ba3eada5ce136516f378971.png)


![g'(x) = \frac{d}{dx}\left[\int_{1}^{x} \frac{1}{{t}^{3}+1} dt \right] g'(x) = \frac{d}{dx}\left[\int_{1}^{x} \frac{1}{{t}^{3}+1} dt \right]](/latexrender/pictures/b0000dc613623b6810004b219d50188a.png)




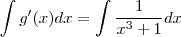


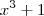 por
por  , teremos:
, teremos: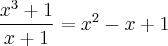
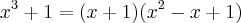
 temos:
temos: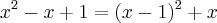
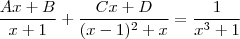
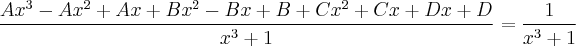
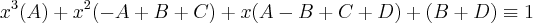
![A = 0 ;\;\;\;\;[1] A = 0 ;\;\;\;\;[1]](/latexrender/pictures/4c8fb4e5a4902dd9f3abf4a0888eb2ef.png)
![A - B + C + D = 0 \;\;\;\;\; [2] A - B + C + D = 0 \;\;\;\;\; [2]](/latexrender/pictures/7446e5abfd3f534fc4a54cabde699199.png)
![-A + B + C = 0 \;\;\;\;\; [3] -A + B + C = 0 \;\;\;\;\; [3]](/latexrender/pictures/cb296d6eae3acf77b20813c009fb817a.png)
![B + D =1 \;\;\;\;\;[4] B + D =1 \;\;\;\;\;[4]](/latexrender/pictures/5711a3e0ae67c5afea8b0031a3ae4db0.png)


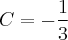
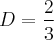
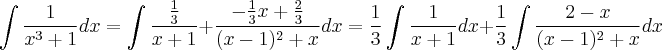
![\frac{1}{3}\int \frac{1}{x + 1} dx = \frac{1}{3} \ln |x+1| + c_{1} \;\;\;\;\; [5] \frac{1}{3}\int \frac{1}{x + 1} dx = \frac{1}{3} \ln |x+1| + c_{1} \;\;\;\;\; [5]](/latexrender/pictures/23c0efbfe1bdec61979300dc3bae36eb.png)
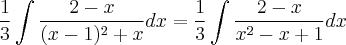
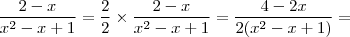
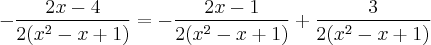


![=-\frac{1}{6}\int \frac{2x - 1}{x^2 - x + 1}dx + \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\;\;[6] =-\frac{1}{6}\int \frac{2x - 1}{x^2 - x + 1}dx + \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\;\;[6]](/latexrender/pictures/b42d4bcbb05714f088cb81ef6d466930.png)



![= -\frac{1}{6} \ln |x^2 - x + 1| + c_{2} \;\;\;\;\; [7] = -\frac{1}{6} \ln |x^2 - x + 1| + c_{2} \;\;\;\;\; [7]](/latexrender/pictures/dd86ecb758e06b42d81db1f85d3a08cf.png)
![\frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\; [8] \frac{1}{2}\int \frac{1}{x^2 - x + 1} dx \;\;\;\;\; [8]](/latexrender/pictures/320eb1c3ce5d24af85e063ca12078043.png)
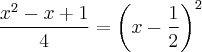
![u = x - \frac{1}{2} \Rightarrow du = dx \;\;\;\; [9] u = x - \frac{1}{2} \Rightarrow du = dx \;\;\;\; [9]](/latexrender/pictures/d29990536b80197d4839453fef30f708.png)
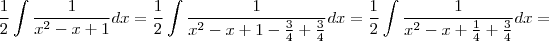

![= \frac{1}{2}\int \frac{4}{4u^{2} + 3} dx \;\;\;\;\;[10] = \frac{1}{2}\int \frac{4}{4u^{2} + 3} dx \;\;\;\;\;[10]](/latexrender/pictures/5c1fdfc811ddd7445f490e7ebdac5f0c.png)
![u = \frac{\sqrt{3}}{2}\tan \theta \Rightarrow du = \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta \;\;\;\;\; [11] u = \frac{\sqrt{3}}{2}\tan \theta \Rightarrow du = \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta \;\;\;\;\; [11]](/latexrender/pictures/84da24cf05eeda82c8ffb829778d64ee.png)
![= \frac{1}{2}\int \frac{4}{3\left[\left( \frac{\sqrt{3}}{2}\tan \theta \right)^2 + \frac{3}{4} \right]} \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta = \int \frac{\sqrt{3}\sec^{2} \theta }{\frac{9}{4}\left( \tan^{2} + 1 \right)} d\theta = = \frac{1}{2}\int \frac{4}{3\left[\left( \frac{\sqrt{3}}{2}\tan \theta \right)^2 + \frac{3}{4} \right]} \frac{\sqrt{3}}{2} \sec^{2} \theta d\theta = \int \frac{\sqrt{3}\sec^{2} \theta }{\frac{9}{4}\left( \tan^{2} + 1 \right)} d\theta =](/latexrender/pictures/97221aed7cb73ee0aec5d011b5087d83.png)
![\int \frac{4\sqrt{3}\sec^{2} \theta }{9\sec^{2}} d\theta = \frac{4\sqrt{3}}{9} \theta + c_{3} \;\;\;\;\; [12] \int \frac{4\sqrt{3}\sec^{2} \theta }{9\sec^{2}} d\theta = \frac{4\sqrt{3}}{9} \theta + c_{3} \;\;\;\;\; [12]](/latexrender/pictures/1dd4528e9d58237accb50be0c02dc467.png)

![\Rightarrow \tan \theta = \frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \Rightarrow \theta = \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] \Rightarrow \tan \theta = \frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \Rightarrow \theta = \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right]](/latexrender/pictures/4e999e0fe33bcf95657b1808839fce99.png)
![= \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + c_{3} \;\;\;\;\; [13] = \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + c_{3} \;\;\;\;\; [13]](/latexrender/pictures/c33b5b2fc9fd861ee55e722391cd9581.png)

![= \frac{1}{3} \ln |x+1| - \frac{1}{6} \ln |x^2 - x + 1| + \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + C = \frac{1}{3} \ln |x+1| - \frac{1}{6} \ln |x^2 - x + 1| + \frac{4\sqrt{3}}{9} \arctan \left[\frac{2\sqrt{3}}{3}\left(x - \frac{1}{2} \right) \right] + C](/latexrender/pictures/bca70d7038848ea24448e32f72d0e507.png)




