1-Como A e B (juntos) recebem o dobro de C, então C receberá 9 e A e B receberão juntos 18 livros.
C poderá receber 9 livros de

modos.
Uma vez que C já recebeu seus livros, teremos 19 modos para distribuir os livros do par AB.
Temos como opções para AB:(0,18),(1,17),(2,16) ... (18,0).
E portanto, para distribuir os livros teremos
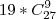
2-Vamos chamar as cores amarela e azul de cores especiais, e tratar a quantidade de cores verde e vermelha pelo par ordenado (vd,vm)
Para pintar 6 bolas com cores especiais, teremos 5 modos diferentes de pintar as outras bolas.(0,4),(1,3)...(4,0),
e logo, 5 modos.
Para pintar 5 bolas com cores especiais( 3az e 2 am, ou 2az e 3am ), teremos 6 modos diferentes de pintar as outras bolas.(0,5),(1,4)...(5,0),
e logo 2* 6 modos. Logo, 12 modos
Para pintar 4 bolas com cores especiais( 3az e 1 am, ou 2az e 2am ou 1az e 3 am), teremos 7 modos diferentes de pintar as outras bolas.(0,6),(1,5)...(6,0),
e logo 3* 7 modos.Logo, 21 modos.
Para pintar 3 bolas com cores especiais( 3az ou 2az e 1 am ou 1 az e 2 am ou 3am ), teremos 8 modos diferentes de pintar as outras bolas.(0,7),(1,6)...(7,0),
e logo 4* 8 modos.Logo, 32 modos.
Para pintar 2 bolas com cores especiais( 2 az ou 1z e 1 am ou 2am ), teremos 9 modos diferentes de pintar as outras bolas.(0,8),(1,7)...(8,0),
e logo 3* 9 modos.Logo, 27 modos.
Para pintar 1 bola com cor especial ( 1 am ou 1 az ), teremos 10 modos diferentes de pintar as outras bolas.(0,9),(1,8)...(9,0),
e logo 2* 10 modos.Logo, 10 modos.
Sem usar cor especial, teremos 11 modos diferentes de pintar as outras bolas.(0,10),(1,9)...(10,0),
e logo 11 modos.
Teremos ao todo:
5+12+21+32+27+10+11= 118 modos diferentes!!!!
3-Considere I(j) o conjunto dos anagramas onde o i aparece junto, e S(j) o conjunto dos anagramas onde o s aparece junto.
Temos então:
#I(j)=8!/2, pois considerando o par de i´s como uma letra teremos
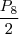
#S(j)=8!/2, pois considerando o par de s´s como uma letra teremos
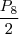
![\#[I(j)\bigcap S(j)]=\frac{7!}{2*2} \#[I(j)\bigcap S(j)]=\frac{7!}{2*2}](/latexrender/pictures/5b0868180f55c46150401fc602ed3710.png)
,pois considerando o par de i´s como uma letra e o par de s´s como uma letra teremos
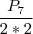
Observe que acima as letras iguais podem ser trocadas de posição, e por isso, para cada letra igual, dividimos a quantidade de anagramas por 2.
![\#[I(j)\bigcup S(j)]= #I(j)+#S(j)-\#[I(j)\bigcap S(j)] \#[I(j)\bigcup S(j)]= #I(j)+#S(j)-\#[I(j)\bigcap S(j)]](/latexrender/pictures/089cdaab8c3235f78ae8fd12b386dbd3.png)
![\#[I(j)\bigcup S(j)]= \frac{8!}{2}+\frac{8!}{2}-\frac{7!}{2*2} \#[I(j)\bigcup S(j)]= \frac{8!}{2}+\frac{8!}{2}-\frac{7!}{2*2}](/latexrender/pictures/aa080f7e0802ab98882f9d373e920b7e.png)
=39.060
Ufaaaaaaaaaaaaaaaaaa!!!!!
Grande abraço!!! Fuiiiiii!!!!!


 modos.
modos.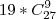
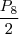
![\#[I(j)\bigcap S(j)]=\frac{7!}{2*2} \#[I(j)\bigcap S(j)]=\frac{7!}{2*2}](/latexrender/pictures/5b0868180f55c46150401fc602ed3710.png) ,pois considerando o par de i´s como uma letra e o par de s´s como uma letra teremos
,pois considerando o par de i´s como uma letra e o par de s´s como uma letra teremos 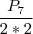
![\#[I(j)\bigcup S(j)]= #I(j)+#S(j)-\#[I(j)\bigcap S(j)] \#[I(j)\bigcup S(j)]= #I(j)+#S(j)-\#[I(j)\bigcap S(j)]](/latexrender/pictures/089cdaab8c3235f78ae8fd12b386dbd3.png)
![\#[I(j)\bigcup S(j)]= \frac{8!}{2}+\frac{8!}{2}-\frac{7!}{2*2} \#[I(j)\bigcup S(j)]= \frac{8!}{2}+\frac{8!}{2}-\frac{7!}{2*2}](/latexrender/pictures/aa080f7e0802ab98882f9d373e920b7e.png)

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)