Poderia alguém me dizer como chegar na fórmula da soma:
Sn=1^2 + 2^2 + ... + n^2 = (n(n+1)(2n+1))/6
Agradeço!





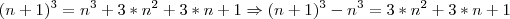
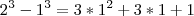
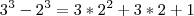

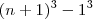 .
.
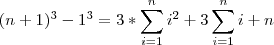 , e logo,
, e logo,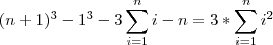 . Desenvolvendo,
. Desenvolvendo,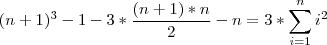 .
.
 =
=
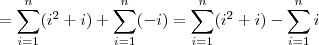
![=\sum_{i=1}^{n}[i(i+1)]-\sum_{i=1}^{n}i =\sum_{i=1}^{n}[i(i+1)]-\sum_{i=1}^{n}i](/latexrender/pictures/b4b53afde0b777c1081c856007d27994.png)

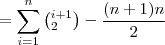
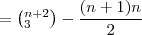

Voltar para Análise Combinatória
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)