 por solon » Ter Jul 14, 2015 03:00
por solon » Ter Jul 14, 2015 03:00
olá, este é o meu primeiro contato com a equipe ajuda Matemática, queria desde já agradecer por esta oportunidade grandiosa de poder interagir com uma comunidade matemática, para que possa haver uma troca mútua de informações, que de certa forma estaremos contribuindo com a difusão do conhecimento. Tenho uma dúvida com relação a como encontrar a razão de uma progressão geométrica da seguinte forma: para 0<a<1, a soma algébrica a-a/2+a^2-a/2^2+a^3-a/2^3+...a^n-a/2^n+...vale:, a reposta correta é a seguinte: a^2/1-a . Já utilizei algumas das propriedades das progressões mas não consegui encontrar o resultado, acredito ter que primeiramente encontrar a razão. Preciso que me mostre um método de resolução para o tal enunciado. Agradeço pela compreensão.
-
solon
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Jul 14, 2015 02:02
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por nakagumahissao » Ter Jul 14, 2015 10:40
por nakagumahissao » Ter Jul 14, 2015 10:40
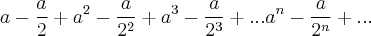
Nesta sequência, podemos observar duas sequências em Progressão Geométrica:
[1]
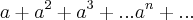
e
[2]
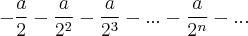
A fórmula da soma de uma PG infinita é:
[3]
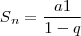
Sendo "n" um número que identifique a soma infinita da sequência 1 ou da Sequência 2.
De [1] e [2], tem-se que:
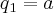
(Obtem-se este valor acima para a razão, dividindo-se a^2 por a, a^3 por a^2, a^4 por a^3 ou quaisquer valores subsequentes pelo seu anterior)
Desta mesma forma:
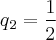
Usando as razões obtidas em [3] e somando-se as duas somas teremos:
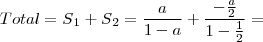
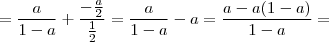
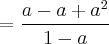
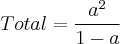

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Progressões
por Cleyson007 » Sáb Set 26, 2009 19:23
- 3 Respostas
- 9234 Exibições
- Última mensagem por shirata

Seg Out 05, 2009 12:18
Progressões
-
- Progressões
por Marcos Roberto » Sáb Out 15, 2011 21:57
- 0 Respostas
- 1494 Exibições
- Última mensagem por Marcos Roberto

Sáb Out 15, 2011 21:57
Progressões
-
- Progressões
por zenildo » Qui Out 10, 2013 22:54
- 1 Respostas
- 1963 Exibições
- Última mensagem por Cleyson007

Sex Out 11, 2013 15:27
Progressões
-
- Progressões
por verilane souza » Ter Set 30, 2014 16:32
- 1 Respostas
- 2102 Exibições
- Última mensagem por fff

Ter Set 30, 2014 18:22
Progressões
-
- progressões
por solon » Qui Jul 23, 2015 17:57
- 2 Respostas
- 4359 Exibições
- Última mensagem por solon

Sáb Ago 01, 2015 03:48
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



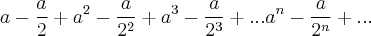
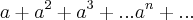
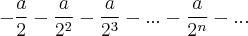
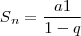
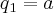
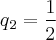
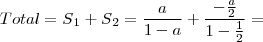
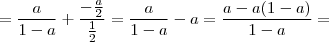
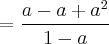
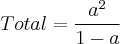



 .
.



