 por Debora Bruna » Sex Jun 26, 2015 23:02
por Debora Bruna » Sex Jun 26, 2015 23:02
Minha vida foi sempre movida na frase de Sócrates "Só sei que nada sei", quanto mais eu estudo mais percebo que não sei de nada.

Seguinte, sempre resolvi questões horrendas, mas hoje inventei tirar à prova do que estou fazendo e me confundi toda.
Problemas como esse, resolvia assim: (?-3)^2 = (corta o expoente com a raiz) = -3.
Mas sei que um número elevado a n é esse número multiplicado n vezes: (?-3)^2 = (?-3).(?-3)= (?-3.-3) = ?9 = 3. Viram? Deu 3 positivo. Assim eu lhes pergunto, onde foi que eu errei?
-
Debora Bruna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Dez 15, 2014 17:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Sáb Jun 27, 2015 14:30
por DanielFerreira » Sáb Jun 27, 2015 14:30
Olá
Débora, boa tarde!
Sua dúvida está relacionada ao estudo do
módulo.
Supomos que queiramos encontrar a raiz quadrada de
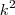
, isto é
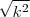
. Veja o que acontece...
Resolução:

Outro exemplo:
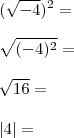
Uma vez que

, temos que

Vale ressaltar que não existe raiz quadrada de números negativos, em

, por isso não podemos cortar a raiz com o expoente!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Debora Bruna » Dom Jun 28, 2015 15:10
por Debora Bruna » Dom Jun 28, 2015 15:10
Muitíssimo obrigada
danjr5 
, esse negócio de corta corta de alguns professores nunca dá certo não é msm?, mas enfim, nunca mais errarei!
-
Debora Bruna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Dez 15, 2014 17:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Dom Jun 28, 2015 16:01
por DanielFerreira » Dom Jun 28, 2015 16:01
Não há de quê e volte sempre!!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- duvida SEndo negativo
por rodrigoyuri » Qui Mai 16, 2013 13:23
- 0 Respostas
- 2765 Exibições
- Última mensagem por rodrigoyuri

Qui Mai 16, 2013 13:23
Binômio de Newton
-
- Todo número negativo é ímpar
por alexandre32100 » Qui Ago 19, 2010 14:53
- 4 Respostas
- 10271 Exibições
- Última mensagem por LuizAquino

Sáb Fev 19, 2011 13:34
Desafios Médios
-
- Limite com raíz cubica sendo o denominador x
por danivelosor » Sáb Mar 28, 2015 21:49
- 1 Respostas
- 2493 Exibições
- Última mensagem por DanielFerreira

Sáb Abr 04, 2015 18:48
Cálculo: Limites, Derivadas e Integrais
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2282 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- Quadrado da raiz quadrada
 por liam gallagher » Qua Nov 11, 2009 23:54
por liam gallagher » Qua Nov 11, 2009 23:54
- 32 Respostas
- 98067 Exibições
- Última mensagem por Rodriguinho

Sex Nov 27, 2009 19:13
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



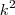 , isto é
, isto é 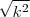 . Veja o que acontece...
. Veja o que acontece...
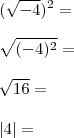
 , temos que
, temos que 
 , por isso não podemos cortar a raiz com o expoente!
, por isso não podemos cortar a raiz com o expoente!
 , esse negócio de corta corta de alguns professores nunca dá certo não é msm?, mas enfim, nunca mais errarei!
, esse negócio de corta corta de alguns professores nunca dá certo não é msm?, mas enfim, nunca mais errarei!

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.