Vestibular Cederj Potencia e Frações

por **lero2007** » Sex Jun 26, 2015 14:25

Olá a todos. Estou com problemas para resolver a seguinte questão:
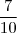Sabendo-se que 2,777... = 2 + $\frac{7} {10}$ + $\frac {7}{10^2}$ + ...
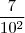e 0,111... = 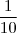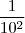$\frac{1} {10}$ + $\frac{1}{10^2}$ ... conclui-se que 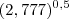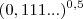$(2,777)^{0,5}$ + $(0,111...)^{0,5}$ é igual a:

(A) 1,444...
(B) 2
(C) 2,888...
(D) 3

Eu tentei a achar a fração motriz de 2,777... e 0,111....
Eu encontrei, respectivamente,
$\frac{25}{9}$ e $\frac{1} {9}$ .

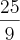Eu manti o expoente inalterado:
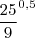$\frac{25}{9}^{0,5}$ e $\frac {1}{9}^{0,5}$

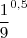
Aí eu tranformei esse 0,5 em fração $\frac{1} {2}$ e fiz a raiz quadrada. Aí q empatei e tentei transformar $\frac {1} {2}$ em $\frac{2} {4}$ Isso é possível? Pq assim consegui resolver, mas nao foi certo.

Obrigado pela atenção de todos

por **Cleyson007** » Sex Jun 26, 2015 15:40

lero2007, boa tarde!

Eu nem cheguei a analisar sua resolução.. Quando você chega em (25/9)^0,5 isso é o mesmo que raiz quadrada de (25/9) = 5/3. Da mesma forma, (1/9)^0,5 é o mesmo que raiz quadrada de (1/9) = 1/3.

5/3 + 1/3 = 6/3 = 2

É essa a dúvida?

por **lero2007** » Sex Jun 26, 2015 16:22

Cleyson007 escreveu:lero2007, boa tarde!

Eu nem cheguei a analisar sua resolução.. Quando você chega em (25/9)^0,5 isso é o mesmo que raiz quadrada de (25/9) = 5/3. Da mesma forma, (1/9)^0,5 é o mesmo que raiz quadrada de (1/9) = 1/3.

5/3 + 1/3 = 6/3 = 2

É essa a dúvida?

Meu deus, cara, como sou estúpido. Putz. Irmão, muito obrigado... Obrigado mesmo!

por **Cleyson007** » Sáb Jun 27, 2015 09:36

Foi um prazer ajudar lero2007 :y:

Precisando estou a disposição!

Caso queira conhecer melhor o nosso serviço nos contacte: viewtopic.php?f=151&t=13614

Abraço e bons estudos

Vestibular Cederj Potencia e Frações

Vestibular Cederj Potencia e Frações

Vestibular Cederj Potencia e Frações

Re: Vestibular Cederj Potencia e Frações

Re: Vestibular Cederj Potencia e Frações

Re: Vestibular Cederj Potencia e Frações

Quem está online