johnatta,
Sempre que postar aqui, por favor, diga-nos o que já tentou fazer para que esta interatividade não seja somente para que você copie o que foi resolvido. Desta forma, nós aqui apenas estaremos resolvendo as questões para você sem que você aproveite alguma coisa. O objetivo deste site é fazer com que cada pessoa aprenda um pouco mais do que sabia antes. Então, por favor, sempre diga-nos por gentileza o que já tentou fazer para resolver o problema, caso contrário, poderá ficar sem ter a ajuda esperada.
Resolução:
Encontre todos os pontos sobre a curva x^2 + y^2 + xy=2 onde a inclinação da reta tangente é -1
Quando dizemos inclinação da reta tangente é -1, queremos dizer que:
[1]

No círculo trigonométrico, existem dois pontos onde isto ocorre: Nos segundos e quartos quadrantes onde:

ou múltiplos deles.
Sabendo-se disto, precisaremos encontrar a derivada de y com relação à y:
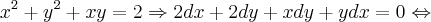
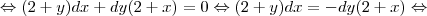

De [1], temos que:
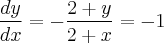

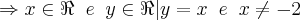

Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali





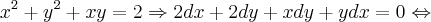
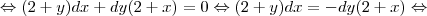

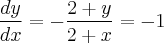

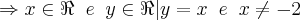




 , avisa que eu resolvo.
, avisa que eu resolvo.

