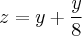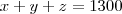por Ana Julia » Seg Jun 01, 2015 21:30
por Ana Julia » Seg Jun 01, 2015 21:30
Guilherme sugeriu distribuir suco de uva para as crianças que participam do Projeto de Responsabilidade
Social. Com o intuito de descobrir o recipiente mais apropriado para conservar o suco, o aluno resolveu
comparar o volume dos três recipientes utilizados no restaurante da escola.
x =Recipiente utilizado
no café da manhã
y=Recipiente utilizado
no lanche
z=Recipiente utilizado
no almoço
Assim, ele observou as seguintes relações entre os três recipientes:
O volume do recipiente do almoço excede em 1/8 o do lanche.
O volume do recipiente do café da manhã excede o do almoço em 650 litros.
O volume dos três recipientes juntos é de 1300 litros.
O volume do recipiente do café da manhã é, em litros:
(A) 600
(B) 650
(C) 800
(D) 875
OBS: COLOCAR PASSO-A-PASSO POR FAVOR
-
Ana Julia
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Jun 01, 2015 20:54
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Ter Jun 02, 2015 19:55
por Cleyson007 » Ter Jun 02, 2015 19:55
Olá Júlia!
Esse tipo de problema é resolvido montando um sistema de equações. Como são três incógnitas (x, y , z) devemos encontrar três equações.
Montei as equações por aqui bem depressa porque tenho compromisso agora às 19:00h.
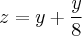

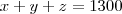
Tente resolver o sistema e me comunique por favor.
Bons estudos.
Caso queira conhecer melhor o nosso trabalho:
viewtopic.php?f=151&t=13614
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda com problema POR FAVOR
por elisamaria » Seg Mar 09, 2015 16:25
- 1 Respostas
- 1528 Exibições
- Última mensagem por Baltuilhe

Qui Abr 02, 2015 20:01
Matemática Financeira
-
- Calcule o volume do solido Confiram Por favor
por Silva339 » Dom Abr 28, 2013 12:10
- 2 Respostas
- 2042 Exibições
- Última mensagem por Silva339

Seg Abr 29, 2013 17:27
Cálculo: Limites, Derivadas e Integrais
-
- Volume de paralelepípedo [problema]
por Netu » Sáb Jan 19, 2013 20:41
- 1 Respostas
- 1942 Exibições
- Última mensagem por DanielFerreira

Sáb Jan 19, 2013 20:56
Geometria Espacial
-
- Volume-ajuda!!
 por Rose » Seg Nov 03, 2008 09:18
por Rose » Seg Nov 03, 2008 09:18
- 1 Respostas
- 2183 Exibições
- Última mensagem por admin

Seg Nov 03, 2008 19:20
Geometria Espacial
-
- Problema sobre PA
por Cleyson007 » Dom Mai 25, 2008 01:53
- 3 Respostas
- 7996 Exibições
- Última mensagem por admin

Dom Mai 25, 2008 04:31
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.