Ajuda Matemática • Exibir tópico - Espaço Vetorial

Anúncio Global

Respostas

Exibições

Última mensagem

Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25

0 Tópicos

606414 Mensagens

Última mensagem por admin
em Qui Nov 15, 2018 00:25
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58

0 Tópicos

547352 Mensagens

Última mensagem por admin
em Qua Nov 14, 2018 11:58
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51

0 Tópicos

778340 Mensagens

Última mensagem por admin
em Ter Mar 20, 2012 21:51
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04

41 Tópicos

2546219 Mensagens

Última mensagem por Janayna
em Qui Abr 27, 2017 00:04

Espaço Vetorial

Regras do fórum

1 mensagem • Página 1 de 1

Espaço Vetorial

por Rosi7 » Sex Mai 29, 2015 20:42

OBRIGADA! JÁ CONSEGUI ENTENDER A QUESTÃO! DESCULPA EU TER POSTADO AQUI, MAS A FACUL ESTÁ EM GREVE E É A SEGUNDA FEZ QUE CURSO ALGEBRA.. E PODE ACREDITAR NÃO TINHA ENTENDIDO ISSO.. BEM AINDA TEM MUITA COISA PRA EU ENTENDER. NÃO SE PREOCUPEM COM ESTA QUESTÃO!

FINALMENTE ENTENDI QUE TEM UMA REGRA À SER SEGUIDA! BJS!

Gente, olhem essa primeira questão: Sendo o gabarito não é espaço, acho que ela está errada, pois pela lógica R1= a+b= b+a.
Sendo que tem outra questão que segue o raciocínio que coloquei aí em cima. $a) \left(x,y \right)+ \left(a,b \right)= \left(x-a,x-b \right) e \alpha\left(x,y \right)=\left(\alphax,\alphay \right) Resposta do gabarito: V1)u+b=v+u \left(x,y \right)+ \left(a,b \right)= (x,y) ii) v+u \left(a+b \right)+(\left( x+y\right)= (a,b) u+v\neq v+u$

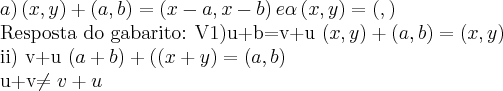
Porém se no R1= a+b= b+a, a "soma" ii) não deveria ter como resposta (x,y)?

Rosi7: Usuário Ativo; Mensagens: 15; Registrado em: Sáb Mai 02, 2015 18:49; Formação Escolar: GRADUAÇÃO; Área/Curso: Licenciatura em Física; Andamento: cursando

1 mensagem • Página 1 de 1

Voltar para Álgebra Linear

Ir para:

Tópicos relacionados

Respostas

Exibições

Última mensagem

Espaço vetorial
por amr » Sex Abr 01, 2011 15:30

4 Respostas

7914 Exibições

Última mensagem por Rosi7
Sáb Mai 30, 2015 00:16
Introdução à Álgebra Linear
Espaço vetorial
por oliveiramerika » Sáb Jan 19, 2013 10:03

1 Respostas

5847 Exibições

Última mensagem por young_jedi
Dom Jan 20, 2013 09:29
Álgebra Linear
Espaço Vetorial
por manuel_pato1 » Sáb Mar 02, 2013 20:03

0 Respostas

1801 Exibições

Última mensagem por manuel_pato1
Sáb Mar 02, 2013 20:03
Álgebra Linear
Espaço Vetorial
por erickm93 » Qui Out 17, 2013 16:48

0 Respostas

1642 Exibições

Última mensagem por erickm93
Qui Out 17, 2013 16:48
Álgebra Linear
[Sub-espaço vetorial]
por JauM » Qua Dez 04, 2013 14:15

2 Respostas

2056 Exibições

Última mensagem por JauM
Qui Dez 05, 2013 14:37
Álgebra Linear

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

Assunto: Unesp - 95 Números Complexos
Autor: Alucard014 - Dom Ago 01, 2010 18:22

(UNESP - 95) Seja L o Afixo de um Número complexo $a=\sqrt{8}+ i$ em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.

Assunto: Unesp - 95 Números Complexos
Autor: MarceloFantini - Qui Ago 05, 2010 17:27

Seja $\alpha$ o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e $\sqrt{8}$ , tal que $tg \alpha = \frac{1}{sqrt{8}}$ . Seja $\theta$ o ângulo complementar. Então $tg \theta = \sqrt{8}$ . Como $\alpha + \theta = \frac{\pi}{2}$ , o ângulo que o afixo

formará com a horizontal será $\theta$ , mas negativo pois tem de ser no quarto quadrante. Se b = x+yi

b = x+yi

, então $\frac{y}{x} = \sqrt {8} \Rightarrow y = x\sqrt{8}$ . Como módulo é um: $|b| = \sqrt { x^2 + y^2 } = 1 \Rightarrow x^2 + y^2 = 1 \Rightarrow x^2 + 8x^2 = 1 \Rightarrow x = \frac{1}{3} \Rightarrow y = \frac{\sqrt{8}}{3}$ .

Logo, o afixo é $b = \frac{1 + i\sqrt{8}}{3}$ .

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.