Estou iniciando meu curso de matemática agora, mas tô com dificuldade numa parte...
Preciso que essa equação se transforme em outra equação de 2º grau. Se alguém puder fazer passo a passo pra mim e explicar o que fez, agradeceria muito!



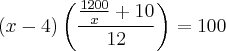
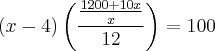
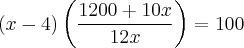
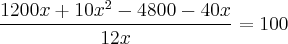
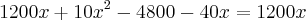
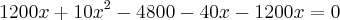
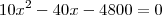
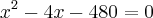
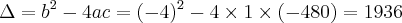
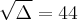
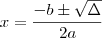
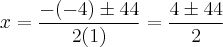
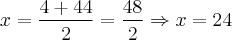
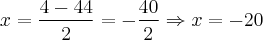

Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes

 .
.



