 por Roni Martins » Ter Fev 16, 2010 13:22
por Roni Martins » Ter Fev 16, 2010 13:22
Opa, boa tarde caros amigos
Preciso da ajuda de voçes para resolver o seguinte problema:
"Na figura a seguir, P é a interseção da bissetriz interna de B com a externa de C. Calcule o angulo BPC em função de A.
figura 2-geometria basica.JPG
-
Roni Martins
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Fev 11, 2010 12:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso de graduação em matemática
- Andamento: cursando
 por Douglasm » Ter Fev 16, 2010 13:37
por Douglasm » Ter Fev 16, 2010 13:37
Boa tarde Roni. Pelo que pude observar:

(soma de dois ângulos internos igual ao externo do outro) e
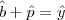
. Sendo assim é só substituir uma fórmula na outra e achar:

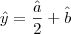
Substituindo na outra equação:
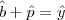
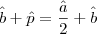

Creio que seja isso. Seria bom se você tivesse o gabarito para conferir!
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Roni Martins » Ter Fev 16, 2010 15:11
por Roni Martins » Ter Fev 16, 2010 15:11
Opa, vlw hein, tu é fera msm, tipo na hora de escrever a duvida, minha net deu um problema e naum deu pra colocar a imagem do exercicio, ate pensei que a duvida não tinha sido postada, mas to vendo que foi postada e vc deu a resposta certim...fikei de boca aberta aki manuw...vlw msm...abraço e tudo de bom...
-
Roni Martins
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Fev 11, 2010 12:34
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso de graduação em matemática
- Andamento: cursando
 por Douglasm » Ter Fev 16, 2010 15:15
por Douglasm » Ter Fev 16, 2010 15:15
Eu achei estranho mesmo...eu vi a imagem uma vez e depois parou de aparecer OO
Mas tranqüilo, estamos aqui pra isso!
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Demonstração envolvendo bissetrizes
por Balanar » Qui Set 02, 2010 00:15
- 0 Respostas
- 1304 Exibições
- Última mensagem por Balanar

Qui Set 02, 2010 00:15
Geometria Plana
-
- Angulos desconhecidos e bissetrizes
por Arthur023 » Sex Mar 02, 2012 11:38
- 2 Respostas
- 3363 Exibições
- Última mensagem por Arthur023

Sáb Mar 03, 2012 20:12
Geometria Plana
-
- Demonstração envolvendo bissetrizes (Confirmar)
por Balanar » Sex Set 03, 2010 19:52
- 0 Respostas
- 1135 Exibições
- Última mensagem por Balanar

Sex Set 03, 2010 19:52
Geometria Plana
-
- Demonstração envolvendo bissetrizes e reta perpendicular
por Balanar » Qui Set 02, 2010 03:07
- 0 Respostas
- 1303 Exibições
- Última mensagem por Balanar

Qui Set 02, 2010 03:07
Geometria Plana
-
- Interseção de Conjuntos
por nietzsche » Dom Jan 16, 2011 16:10
- 12 Respostas
- 6880 Exibições
- Última mensagem por nietzsche

Dom Jun 26, 2011 21:26
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 (soma de dois ângulos internos igual ao externo do outro) e
(soma de dois ângulos internos igual ao externo do outro) e 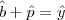 . Sendo assim é só substituir uma fórmula na outra e achar:
. Sendo assim é só substituir uma fórmula na outra e achar:
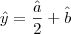
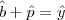
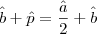





 .
.
 :
: