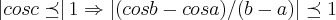por rnts » Qui Abr 30, 2015 22:28
por rnts » Qui Abr 30, 2015 22:28
Olá. Preciso demonstrar algumas desigualdades utilizando o Teorema do Valor Médio. Mas não tenho muita ideia de como aplicá-lo nestes casos.
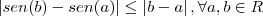
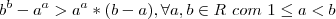
Agradeço caso alguém possa ajudar.
-
rnts
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 27, 2012 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por adauto martins » Sex Mai 01, 2015 20:13
por adauto martins » Sex Mai 01, 2015 20:13
teorama T.V.M...diz...
![\exists c\in [a,b]/f'(c)=f(b)-f(a)/(b-a)\Rightarrow cosc=(senb-sena)/(b-a) \exists c\in [a,b]/f'(c)=f(b)-f(a)/(b-a)\Rightarrow cosc=(senb-sena)/(b-a)](/latexrender/pictures/fc56199157b403fb98f217a72eac979d.png)
como
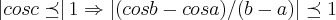
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [VALOR MÉDIO]
por magellanicLMC » Sex Fev 07, 2014 23:05
- 2 Respostas
- 1681 Exibições
- Última mensagem por magellanicLMC

Sáb Fev 08, 2014 17:00
Cálculo: Limites, Derivadas e Integrais
-
- Valor médio
 por Janoca » Ter Jun 17, 2014 01:05
por Janoca » Ter Jun 17, 2014 01:05
- 7 Respostas
- 5068 Exibições
- Última mensagem por alienante

Qua Jun 18, 2014 18:11
Cálculo: Limites, Derivadas e Integrais
-
- teorema do valor medio
por matmatco » Seg Nov 14, 2011 10:18
- 3 Respostas
- 2677 Exibições
- Última mensagem por LuizAquino

Seg Nov 14, 2011 20:46
Cálculo: Limites, Derivadas e Integrais
-
- Teorema do valor médio
por crsjcarlos » Qua Mai 01, 2013 12:09
- 1 Respostas
- 1987 Exibições
- Última mensagem por e8group

Qua Mai 01, 2013 14:07
Cálculo: Limites, Derivadas e Integrais
-
- [teorema do valor médio]
por Ge_dutra » Seg Jun 17, 2013 00:12
- 0 Respostas
- 1215 Exibições
- Última mensagem por Ge_dutra

Seg Jun 17, 2013 00:12
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
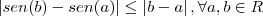
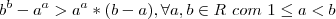

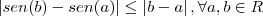
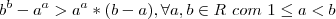

![\exists c\in [a,b]/f'(c)=f(b)-f(a)/(b-a)\Rightarrow cosc=(senb-sena)/(b-a) \exists c\in [a,b]/f'(c)=f(b)-f(a)/(b-a)\Rightarrow cosc=(senb-sena)/(b-a)](/latexrender/pictures/fc56199157b403fb98f217a72eac979d.png)