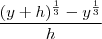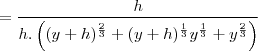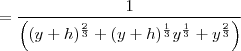por Zeh Edu » Qua Abr 29, 2015 08:40
por Zeh Edu » Qua Abr 29, 2015 08:40
Galera, preciso fatorar a seguinte expressão e não sei por onde começar
( (y+h)^(1/3) - y^(1/3) )/h
Desde já, muito obrigado pela ajuda

-
Zeh Edu
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mai 08, 2012 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando para engenharia
- Andamento: cursando
 por young_jedi » Qua Abr 29, 2015 19:50
por young_jedi » Qua Abr 29, 2015 19:50
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Zeh Edu » Qui Abr 30, 2015 00:31
por Zeh Edu » Qui Abr 30, 2015 00:31
Young Jedi, é isso mesmo. Preciso calcular o limite daquela expressão quando h tende a zero. Mas fiquei perdido quando vi a diferença de elementos com raiz cúbica. Nesses casos fica mais fácil deixar elevado à fração ?
O raciocínio que você usou tem a ver com triângulo de pascal ? Ou então é parecido com a fatoração de uma soma ou diferença elevado a um n.
(a+b)^n = (a+b)*( a^(n-1)*b^0 + a^(n-2)*b^1 + ... + a^0*b^(n-1) )
(a+b)^5 = (a+b)(a^4 + a^3*b + a^2*b^2 + a*b^3 + b^4)
quando se tem (a+b) elevado a uma fração não entendi muito bem como se fatora. Existe algum material com o qual eu possa estudar isso com mais profundidade ?
Obrigado Young Jedi, e que a força esteja com vc

-
Zeh Edu
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mai 08, 2012 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando para engenharia
- Andamento: cursando
 por young_jedi » Qui Abr 30, 2015 21:27
por young_jedi » Qui Abr 30, 2015 21:27
Então
Zeh Edueu utilizei a seguinte igualdade

neste nosso caso
n=3

e

o objetivo aqui era "tirar" aquele expoente 1/3 para poder simplificar por isso o n escolhido foi 3
no resultado final aparecem elemento com expoente contendo raiz cubica, mas isso não tem problema na hora de calcular o limite, pois o importante era simplificar o h do denominador com o do numerador
como material eu recomento so livro do Stewart que acho muito bom
e esses dois site são bons também
http://ecalculo.if.usp.br/index.htmhttp://pessoal.sercomtel.com.br/matematica/superior/superior.htme este video do youtube explica bem essa parte que eu mostrei
https://www.youtube.com/watch?v=taF5XZfgYBc
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Zeh Edu » Qui Abr 30, 2015 23:35
por Zeh Edu » Qui Abr 30, 2015 23:35
Entendi Jedi, valeu pela ajuda!!

-
Zeh Edu
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Ter Mai 08, 2012 01:35
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Vestibulando para engenharia
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatoração de raiz cúbica
por Paula Noia » Sáb Jun 15, 2013 21:22
- 2 Respostas
- 12282 Exibições
- Última mensagem por Paula Noia

Dom Jun 16, 2013 11:29
Cálculo: Limites, Derivadas e Integrais
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7440 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- log na base 1\5 de raiz cubica de 625 = 2x
por Nessa 2012 » Seg Nov 19, 2012 16:18
- 1 Respostas
- 3577 Exibições
- Última mensagem por Cleyson007

Seg Nov 19, 2012 16:31
Logaritmos
-
- Limite raiz cúbica
por Carolminera » Qua Jul 16, 2014 18:25
- 0 Respostas
- 3551 Exibições
- Última mensagem por Carolminera

Qua Jul 16, 2014 18:25
Cálculo: Limites, Derivadas e Integrais
-
- Limite com raíz cúbica
por Rosi7 » Sex Ago 07, 2015 21:34
- 2 Respostas
- 8419 Exibições
- Última mensagem por Rosi7

Seg Ago 10, 2015 13:22
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.